Dans ce chapitre, nous allons étudier en détail les méthodes qui favorisent la structure locale du phénomène observé. L’objectif n’est donc pas de retrouver la variété globale d’origine, mais de souligner certains comportement des données à l’échelle locale.
Problème avec l'ACP et les méthodes globales
Comme on l’a vu précédemment, l’analyse par composantes principales essaie de déterminer la structure sous-jacente d’un jeu de données. Pour rappel, l’ACP maximise la variance, en minimisant l’erreur en distance euclidienne entre les données originales et la projection.
Parce qu’on utilise une erreur quadratique, seules les grandes distances/variations entre les données sont magnifiées, et “écrasent” rapidement les petites variations.
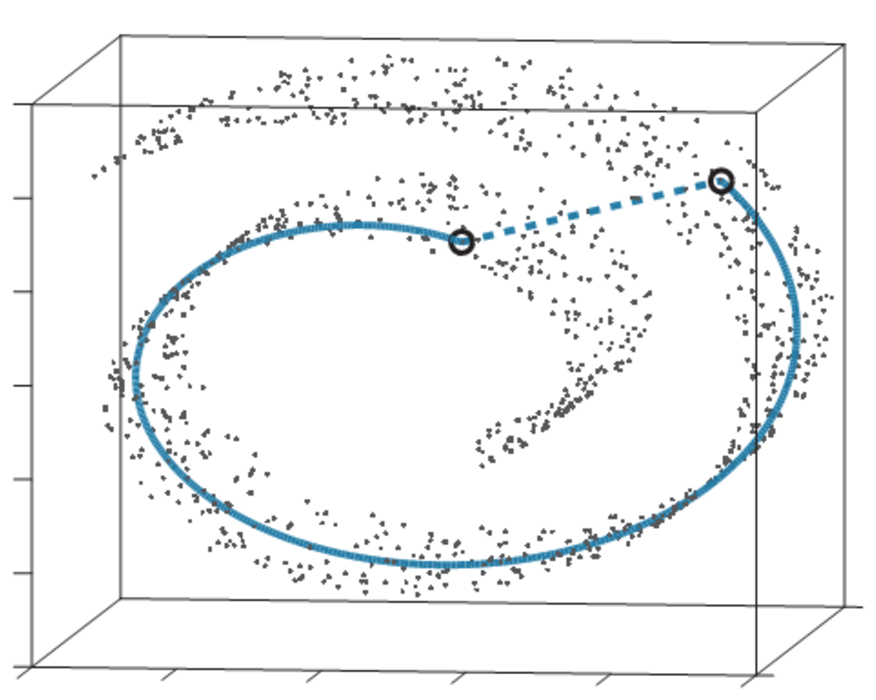
Les points ici sont proches dans l’espace euclidien (en pointillés, la distance euclidienne) mais éloignés si on considère le jeu de données (en trait plein, la distance “selon les données”).
L’idée des algorithmes de ce chapitre est de considérer la variété (manifold, en anglais) tout entière, et de se concentrer sur la structure locale des données, en mettant en exergue cette fois les paires de distances euclidiennes entre les points proches.
On gagne ainsi deux avantages principaux :
en travaillant seulement à l’échelle locale, on travaille avec beaucoup moins de points sur nos calculs, donc un gain en complexité algorithmique non négligeable ;
on aura une meilleure représentation d’un plus grand nombre de variétés, dont la géométrie générale est trop éloignée d’une représentation euclidienne pour pouvoir être utile. En se libérant de cette contrainte générale, on ouvre ainsi la possibilité d'une représentation plus fidèle sur une plus large classe de variétés.
LLE (Locally Linear Embedding)
On commence à y être habitués, on veut trouver une représentation de dimension inférieure de nos points . Cette fois-ci, en revanche, on ne va travailler que sur le voisinage des points.
La technique de LLE (qui est apparue dans le même journal qu'Isomap, d’ailleurs), consiste à effectuer deux optimisations.
La première, c’est, dans l’espace d’origine à grande dimension, de trouver comment reconstruire chaque point à l’aide de ses K plus proches voisins, en minimisant la fonction suivante :
où V(X) représente la matrice des K voisins de X. On obtient ainsi la matrice W.
À l’aide de cette matrice, on veut trouver les points Y dans la variété de dimension inférieure en minimisant :
Et voilà ! C’est facile, hein ! 😀
C’est une première méthode assez classique de visualisation de données non linéaire. En général, la variété se retrouve représentée le long d’axes qui représentent les degrés de liberté principaux du phénomène.
t-SNE (t-Stochastic Neighbor Embedding)
Dans cette partie, nous allons étudier une des méthodes de visualisation les plus usitées en ce moment, t-SNE, pour “t-distributed Stochastic Neighbor Embedding”. Le t désigne une distribution utilisée dans l’algorithme (pour loi t de Student ; on verra plus tard pourquoi).
En bref, cette technique permet de visualiser des données de (très) grandes dimensions, en effectuant un plongement (embedding, en anglais) dans une variété de plus petite dimension, généralement 2 ou 3 pour pouvoir repérer des caractéristiques intéressantes du phénomène à modéliser. Elle est devenue populaire pour sa capacité à générer des visualisations très parlantes.

Intuition du fonctionnement
Comme je l’ai dit plus haut, le t-SNE met l’accent sur les petites distances. Le concept général de l’algorithme est de considérer chaque point de données séparément, et d’assigner une probabilité conditionnelle (un poids) gaussienne à chacun des autres points en fonction de sa distance par rapport à ce point.
Une fois toutes ces probabilités calculées , on peut plonger dans une dimension inférieure ce jeu de données en calculant une nouvelle distribution (qui est une t-student distribution cette fois, d’où le “t”), qui minimise la KL divergence entre P et Q.
L’idée est de trouver un espace de dimension inférieure, mais qui respecte une distribution proche en KL divergence de la distribution d’origine.
Encore une fois, la probabilité met l’accent sur la structure locale, puisqu’elle met plus de poids sur les petites distances entre les points du jeu de données.
On peut par exemple appliquer t-SNE sur le jeu de données de visages (Olivetti dataset).
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_olivetti_faces
from sklearn import (manifold, datasets, decomposition, ensemble,discriminant_analysis, random_projection)
from matplotlib import offsetbox
olivetti = fetch_olivetti_faces()
targets = olivetti.target
data = olivetti.data
images = olivetti.images
# fonction pour afficher une partie des images sur la visualisation 2D
def plot_embedding(X, title=None):
x_min, x_max = np.min(X, 0), np.max(X, 0)
X = (X - x_min) / (x_max - x_min)
plt.figure(figsize=(15, 15))
ax = plt.subplot(111)
if hasattr(offsetbox, 'AnnotationBbox'):
shown_images = np.array([[1., 1.]])
for i in range(data.shape[0]):
dist = np.sum((X[i] - shown_images) ** 2, 1)
if np.min(dist) < 2e-3:
continue
shown_images = np.r_[shown_images, [X[i]]]
props={ 'boxstyle':'round', 'edgecolor':'white'}
imagebox = offsetbox.AnnotationBbox(offsetbox.OffsetImage(images[i], cmap=plt.cm.gray, zoom=0.5), X[i], bboxprops=props)
ax.add_artist(imagebox)
if title is not None:
plt.title(title)
X = data
tsne = manifold.TSNE(n_components=2, perplexity=40, n_iter=3000, init='pca')
X_tsne = tsne.fit_transform(X)
plot_embedding(X_tsne, "Principal Components projection of the digits")
plt.show()
Comme on peut le voir, t-SNE permet de distinguer différents clusters, associés aux différents visages, sans supervision ! Vous pouvez essayer de reproduire une visualisation similaire à l'aide de différents hyperparamètres (perplexité, nombre d'itérations).
Utilisation en pratique
Maintenant que vous avez une intuition du fonctionnement du t-SNE, on va voir comment l’utiliser en pratique, et dans quelles circonstances il sera le plus pertinent.
Attends, mais ce n’est pas censé être un algorithme non supervisé ? Je ne suis pas censé appuyer sur un bouton magique et avoir mon résultat ?
Même si c’est un algorithme non supervisé, il demande de développer une petite intuition de son fonctionnement et des différents comportements sur des cas simples, afin de pouvoir comprendre un peu mieux les visualisations créées, et les interpréter correctement.
Perplexité
Il y a une notion que je n’ai pas évoquée dans l’explication sur le fonctionnement du t-SNE : c'est la notion de perplexité, que vous allez devoir fixer pour utiliser l’algorithme. La perplexité représente en fait la taille de la variance de . Grosso modo, elle représente la balance entre prise en compte de la structure globale et celle de la structure locale, c’est-à-dire une estimation du nombre de voisins “proches” (relativement à l’ensemble du jeu de données) que possède chaque point.
De fait, vous pouvez tester une valeur de la perplexité entre 5 et 50 à partir de 5-10 k observations.
Visualisation du dataset
t-SNE permet de visualiser la structure des données à très hautes dimensions, afin de pouvoir orienter par la suite la modélisation.
Alors, que représente cette visualisation du jeu de données ?
Eh bien, la principale chose qu’on peut distinguer sur le t-SNE, ce sont les différents clusters créés, qui peuvent représenter plusieurs catégories de données qui ont été détectées. Comme les chiffres sur l’image plus haut, par exemple.
La seconde chose qui peut arriver, c’est que l’ordre relatif des différentes observations peut représenter une feature sous-jacente. Par exemple, j’ai zoomé ci-dessous sur le cluster de “1” d’une visualisation t-SNE des données MNIST. Comme on peut le voir, les 1 sont organisés selon leur orientation (de légèrement penché vers la gauche à légèrement penché vers la droite).

Si t-SNE vous fournit un clustering satisfaisant (avec des groupes assez bien séparés) par rapport à une PCA linéaire classique, cela veut dire que vous pourrez utiliser des algorithmes supervisés favorisant cette structure locale (comme le SVM, que nous étudierons dans un autre cours).
Validation de features
Visualiser les données, c’est pas mal pour développer une intuition sur notre dataset. Une autre application assez utilisée du t-SNE consiste à valider les features que l’on vient de créer.
En effet, si vous avez créé des features qui vous semblent représentatives des distinctions entre les données, cette distinction doit se retrouver lors de la visualisation du t-SNE. Si vos features ne semblent pas se retrouver groupées de manière significative, c’est peut-être qu’elles ne sont pas si représentatives des similarités/distinctions entre les données, qui vous permettront de les modéliser.
Le t-SNE, dans ce sens, permet de valider que les features créées sont bien représentatives de la topologie du jeu de données, et qu'elles permettront potentiellement une modélisation correcte du phénomène.
Potentiels problèmes
Problèmes d'interprétation
Il existe pléthore d’erreurs d’interprétation possibles, sur tous les autres aspects du phénomène : la taille des clusters n’est pas significative, ni la distance entre les différents clusters, difficile de détecter la topologie (i.e. si une catégorie de points est contenue dans l’autre). Attention à ne pas surinterpréter les visualisations.
Je vous conseille l'excellent article sur le sujet : http://distill.pub/2016/misread-tsne/.
Problèmes de temps de calcul
t-SNE possède une complexité quadratique au nombre de points N, en temps et espace. Ce qui veut dire que ça devient rapidement inutilisable au-delà de quelques milliers/dizaines de milliers de points.
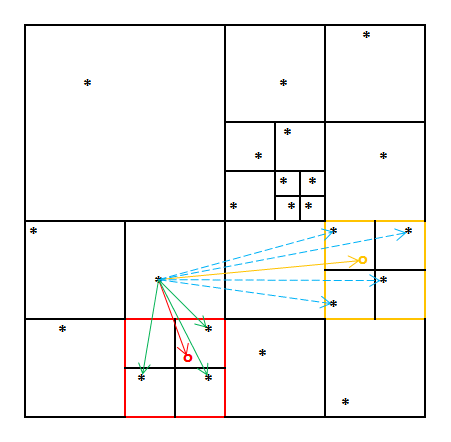
Heureusement, une technique a été développée depuis, qui partitionne l’espace pour optimiser le calcul des différentes . Cette méthode utilise la méthode de Barnes-Hut qui permet de partitionner l’espace afin d’optimiser le calcul des distances entre deux points, qui est le plus lourd en termes de calculs. En utilisant cette méthode d’approximation, t-SNE est applicable sur un gros jeu de données, et passe à une complexité . C’est en fait la méthode recommandée, qui est déjà implémentée dans la fonction t-SNE de Scikit. 😱
Données métriques
Il faut faire attention à la nature des données évaluées. En effet, t-SNE n’est pratique que lorsqu’il existe une symétrie entre les données. C’est-à-dire que si un point A est proche de B et que B est proche de C, alors A est proche de C (l’inégalité triangulaire est respectée). Il existe une variante du t-SNE pour ce genre de besoin, à l'aide de plusieurs visualisations (l'article de référence ici).
Quand est-ce que ce n’est pas le cas ?
Un cas simple, qui n’est pas représentable par un t-SNE classique : les données texte. Imaginons que le mot “roi” soit proche de “reine”, et que “reine” soit proche du mot “femme”, ça ne veut pas dire que “roi” est proche de “femme” ! t-SNE ne fera pas cette distinction. Faites donc bien attention à la signification des relations entre les observations.
Pas de préservation de la structure globale
Comme je l’ai dit plus haut, l’algorithme t-SNE a été construit spécifiquement pour mettre en exergue la structure locale du jeu de données. C’est pourquoi il perd facilement la structure globale du dataset, qui peut aussi être utile à visualiser.
L’idée dans ce cas est soit d’utiliser plusieurs visualisations (une t-SNE pour observer la structure locale, et PCA ou Isomap pour la structure globale, par exemple). Une autre solution consiste à initialiser l’algorithme t-SNE par une PCA avant de le lancer, ce qui permet de conserver de base une plus grande part de la structure globale (avec l'option init=’pca’ ).
Résumé
On a vu dans ce chapitre l’algorithme t-SNE qui est une des méthodes les plus utilisées pour visualiser des données à grandes dimensions non linéaires, afin de repérer des structures locales intéressantes pour le travail de modélisation.
Attention encore une fois à bien développer une intuition de ce que peut apporter une visualisation t-SNE, et à bien en faire plusieurs exécutions avec différents hyperparamètres. Il faut tester un bon nombre de fois ces méthodes avec des datasets différents pour bien les prendre en main.
