Entraînez un modèle prédictif linéaire

10 hours
Medium

Free online content available in this course.

course.header.alt.is_video

course.header.alt.is_certifying

Last updated on 8/2/23

Classifiez vos données en plus de deux classes

Supposons maintenant que nous ayons plus de deux classes. Par exemple, un problème de classification d'images entre « voiture », « vélo », « bus de ville », « piéton », « scooter ». Comment utiliser les classifieurs binaires que nous savons construire pour résoudre un tel problème ?

Nos données sont toujours n points en p dimensions, représentés par la matrice $$$X \in \mathbb{R}^{n \times p}$$$ , et leurs étiquettes, $$$y \in \{0, 1, \dots, (K-1)\}.$$$ Nous avons donc K classes.

One-versus-rest

Une première approche consiste à créer un classifieur $$$f_k$$$ pour chacune des classes, qui sépare les points de cette classe de tous les autres points.

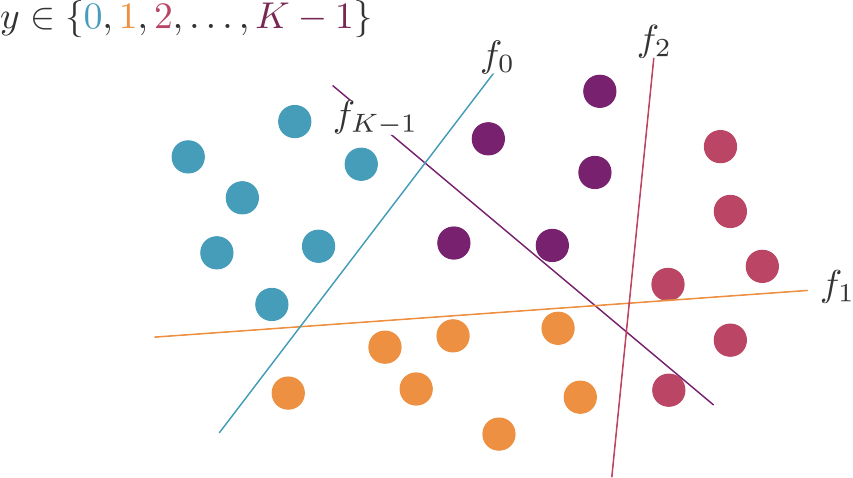
Chaque droite sépare (parfois avec des erreurs) les points d'une classe de tous les autres.

Cette méthode est appelée one-versus-rest (« une contre le reste », OVR en abrégé) ou one-versus-all (« une contre toutes », OVA en abrégé).

Nous avons maintenant K classifieurs. Comment obtenir une seule prédiction finale ?

Supposons que nos classifieurs soient des régressions logistiques. Alors $$$f_k(x) = p(Y=k|x)$$$ , il est logique de prédire que x appartient à la classe pour laquelle cette prédiction est la plus élevée. Dans le cas des SVM, $$$f_k(x)$$$ indique la distance entre x et l'hyperplan qui sépare la classe k des autres. Plus cette valeur est élevée, plus nous sommes convaincus que x appartient à la classe k.

Nous allons donc simplement prédire la classe pour laquelle la fonction de décision retourne la valeur la plus élevée :

$$\[f(x) = \arg\max_{k} f_k(x)\]$$

Complexité algorithmique

Pour entraîner notre algorithme, nous avons dû entraîner K classifieurs sur n points chacun. Si j'appelle $$$C_n$$$ la complexité algorithmique du classifieur de base, la complexité de l'entraînement de notre OVR est donc $$$\mathcal{O}(K C_n).$$$

En ce qui concerne la prédiction, il faut faire K prédictions, puis en prendre le maximum. Nous avons donc une complexité de $$$\mathcal{O}(K C_{\mbox{pred}}),$$$ où $$$C_{\mbox{pred}}$$$ est la complexité de la prédiction d'un de nos classifieurs de base.

OVR est implémenté dans scikit-learn : sklearn.multiclass.OneVsRestClassifier.

One-versus-one

Une autre façon de faire consiste à calculer K(K-1) classifieurs, chacun séparant une classe d'une autre en ignorant les autres classes (et les observations qui leur appartiennent).

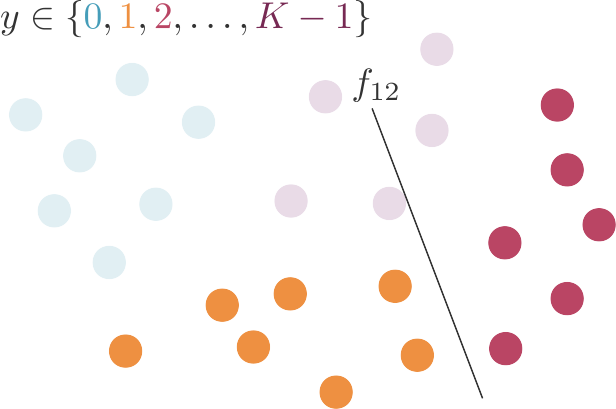
On sépare la classe 1 de la classe 2 en ignorant les autres classes.

Cette méthode est appelée one-versus-one (« une contre une », OVO en abrégé).

Comment fait-on une prédiction maintenant, avec K(K-1) classifieurs ?

Pour prédire, nous allons utiliser un vote de la majorité : la classe prédite est celle retournée par le plus grand nombre de classifieurs.

Complexité algorithmique

Nous devons maintenant construire $$$\frac{K(K-1)}{2}$$$ classifieurs plutôt que K. Nos temps de calcul vont augmenter ! Eh bien, tout dépend de $$$C_n$$$ . Nous entraînons certes $$$\frac{K(K-1)}{2}$$$ classifieurs, mais chacun d'entre eux est entraîné sur $$$\frac{n}{k}$$$ points seulement.

OVO est implémenté dans scikit-learn : sklearn.multiclass.OneVsOneClassifier.

SVM multi-classe

Regardons maintenant de plus près le cas des SVM.

Appliquons l'algorithme OVR dans un contexte multiclasse. Nous allons construire l'un après l'autre K hyperplans séparateurs d'équations $$$f_k(x) = \langle w_k, x \rangle + b_k.$$$ Chacun de ces hyperplans vérifie

$$\[\arg \min_{w_k \in \mathbb{R}^p, b_k \in \mathbb{R}, \xi_k \in \mathbb{R}^n} \frac{1}{2} ||w_k||_2^2 + C \sum_{i=1}^n \xi_{ik}\]$$

avec $$$\xi_{ik} \geq 0 $$$ et $$$\delta(k, y^{(i)}) (\langle w_k, x^{(i)} \rangle + b_k) \geq 1 - \xi_{ik} \,\, \forall i \in \{1, \dots, n\},$$$ où
$$$\delta(k, y^{(i)})$$$ vaut 1 si $$$y^{(i)} = k$$$ et -1 sinon.

Nous avons donc K problèmes d'optimisation à 2n contraintes à résoudre. Chacune des contraintes dit que chaque point $$$x^{(i)}$$$ doit être au pire à une distance $$$\xi_i$$$ du « mauvais côté » de la frontière de la zone d'indécision entre sa classe et l'union des autres classes.

Mais nous pouvons changer la contrainte pour chercher à découvrir les K hyperplans simultanément, de sorte que chaque point du jeu d'entraînement soit (1) du bon côté de l'hyperplan séparateur de sa classe, d'équation $$$f_{y^{(i)}}(x),$$$ et plus loin de cet hyperplan séparateur que de tous les autres, définis par $$$f_k, k \neq y^{(i)}$$$ . Idéalement, nous voudrions donc que pour chaque point $$$x^{(i)},$$$

$$\[\langle w_{y^{(i)}}, x^{(i)} \rangle + b_{y^{(i)}} \geq \langle w_k, x^{(i)} \rangle + b_k + 1, \,\,\, \forall k \neq {y^{(i)}}.\]$$

Comme cela va certainement ne pas être systématiquement possible, on peut réintroduire ici les variables d'ajustement et imposer

$$\[\langle w_{y^{(i)}}, x^{(i)} \rangle + b_{y^{(i)}} \geq \langle w_k, x^{(i)} \rangle + b_k + 1 - \xi_i, \,\,\, \forall k \neq {y^{(i)}}.\]$$

Nous pouvons donc formuler le SVM multi-classe comme le problème suivant, qui utilise n variables $$$ $\xi_i$$$$ au lieu de $$$$nK$$$$ :

$$\[\arg \min_{w \in \mathbb{R}^{K \times p}, b \in \mathbb{R}^K, \xi \in \mathbb{R}^n} \frac{1}{2} ||w_k||_2^2 + C \sum_{i=1}^n \xi_{i}\]$$

avec $$$\xi_{i} \geq 0$$$ et $$$\langle w_{y^{(i)}}, x^{(i)} \rangle + b_{y^{(i)}} \geq \langle w_k, x^{(i)} \rangle + b_k + 1 - \xi_i, \,\,\, \forall k \neq {y^{(i)}}. $$$

Comme dans OVR, la prédiction se fait selon la fonction de décision maximale :

$$\[f(x) = \arg \max_{k \in \{0, \dots, K-1\}} (\langle w_k, x \rangle + b_k).\]$$

Cette méthode a été proposée par Crammer et Singer en 2002. Elle est implémentée dans scikit-learn via l'optionmulti_class="crammer_singer" de sklearn.svm.LinearSVC. Par défaut, LinearSVC gère le multi-classe avec une approche OVR.

Conclusion

L'approche one-versus-rest de la classification multi-classes consiste à créer K classifieurs binaires qui séparent chaque classe k de l'union des autres classes. On prédit alors la classe pour laquelle la fonction de décision est maximale.
L'approche one-versus-one consiste à créer K(K-1) classifieurs binaires qui séparent chacun une classe d'une autre, en ignorant tous les autres points. On utilise alors un vote de la majorité pour prédire. Cette approche crée plus de classifieurs, mais chacun est entraîné sur moins d'observations.
On peut créer des SVM multiclasse en optimisant simultanément K classifieurs binaires (méthode de Crammer et Singer).

Nous verrons aussi dans un prochain cours qu'il existe plusieurs algorithmes non-linéaires qui sont naturellement multi-classes.