Manipulations d'histogrammes
Nous abordons ici les techniques de traitement d'images basées sur la modification d'histogrammes. Ces méthodes font partie de la classe des traitements dits ponctuels : la valeur de chaque pixel est corrigée, et ce indépendamment des autres pixels.
Qu'est ce qu'un histogramme dans le domaine de l'imagerie numérique ?
L'histogramme d'une image numérique est une courbe statistique représentant la répartition de ses pixels selon leur intensité. Pour une image en noir et blanc, il indique en abscisse le niveau de gris (entier entre 0 et 255) et en ordonnée, le nombre de pixels ayant cette valeur.
Lorsque l'histogramme est normalisé, il indique en ordonnée la probabilité de trouver un pixel de niveau de gris dans l'image :
L'intensité d'un pixel est alors vue comme une variable aléatoire discrète.
Un histogramme cumulé normalisé calcule le pourcentage de pixels ayant une valeur inférieure à un niveau de gris donné :
L'histogramme normalisé peut être interprété comme une densité de probabilité, et l'histogramme cumulé normalisé comme la fonction de répartition.
La génération d'histogrammes se fait aisément en Python avec la fonction hist de matplotlib.pyplot :
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
# Charger l'image comme matrice de pixels
img = np.array(Image.open('simba.png'))
# Générer et afficher l'histogramme
# Pour le normaliser : argument density=True dans plt.hist
# Pour avoir l'histogramme cumulé : argument cumulative=True
n, bins, patches = plt.hist(img.flatten(), bins=range(256))
plt.show()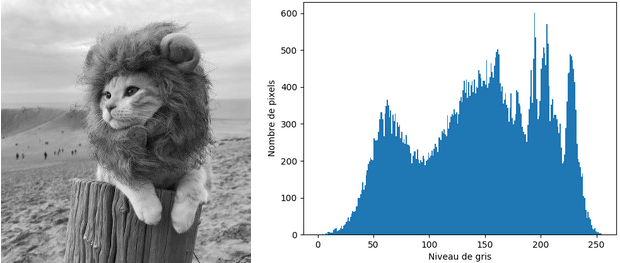
Il s'agit d'un outil très important en traitement d'images, car sa modification permet d'ajuster la dynamique des niveaux de gris ou des couleurs dans une image afin de la rendre plus agréable visuellement. Grossièrement, à gauche se situent les pixels noirs, à droite les pixels blancs, et au milieu, toutes les nuances de gris.
Étirement d’histogrammes
Une première application consiste à corriger la luminosité, ou exposition, de l'image. Analysons la forme des histogrammes pour des images dont l'exposition est mauvaise :
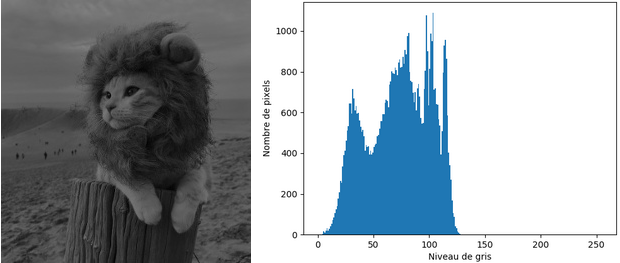
Vous pouvez constater que pour l'image trop sombre, ou sous-exposée, la majorité des pixels se situent dans la partie gauche de l'histogramme, vers les valeurs de niveaux de gris faibles.
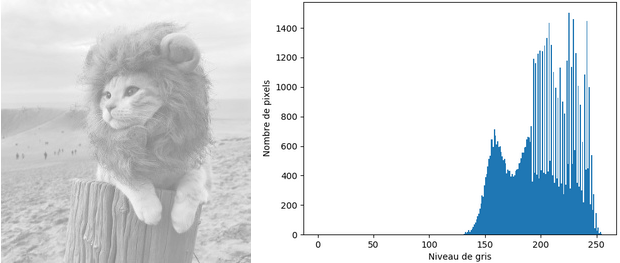
Inversement, les pixels de l'image trop claire, ou sur-exposée, se concentrent dans la partie droite de l'histogramme.
En revanche, l’histogramme associé à l’image dont l’exposition est relativement bonne présente une répartition des pixels sur tout l’intervalle [0,255]. Ainsi, pour corriger les défauts liés à l’exposition d'une image, il suffit simplement d'étirer son histogramme : l'objectif est d'étendre les valeurs des niveaux de gris de l'image mal exposée, majoritairement répartis dans un sous intervalle , à tout l'intervalle disponible.
Cette transformation se fait simplement à l’aide de la règle de trois : la valeur de chaque pixel est remplacée par le résultat de la formule ci-dessous.
où et désignent les intensités du pixel de coordonnées respectivement dans l'image mal exposée et la nouvelle image.
Concrètement, cette formule mathématique signifie qu'on déplace les niveaux de gris de vers , avant de les répartir dans [0,255].
En pratique, et sont souvent déterminées comme les niveaux de gris minimum et maximum de l'image après avoir éliminé 1% des valeurs extrêmes.
Et c'est tout ! L'étirement d'histogramme se fait avec la fonction autocontrastdu module ImageOps de Pillow. On l'applique sur l'image sur-exposée :
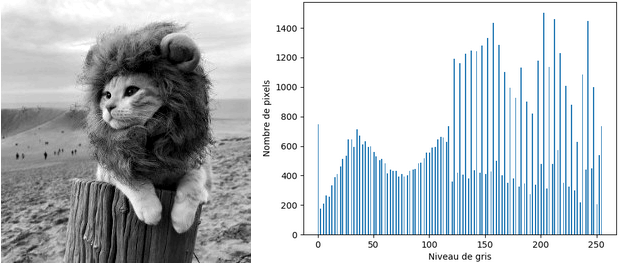
Le résultat est satisfaisant : les pixels se répartissent bien dans tout l'intervalle [0,255] et l'image présente une meilleure luminosité ! En guise de petit exercice, vous pouvez appliquer la transformation sur l'image trop sombre.
Égalisation d’histogrammes
La deuxième application courante concerne l'amélioration du contraste de l'image.
Le contraste caractérise la répartition de lumière dans une image : plus une image est contrastée, plus la différence de luminosité entre ses zones claires et sombres est importante. En général, une image peu contrastée est terne, tandis qu'une image trop contrastée est visuellement "agressive". Dans les deux cas, l'image manque de clarté car certains de ses détails seront peu, voire pas du tout, visibles.
L'égalisation d'histogrammes est une technique simple permettant de réajuster le contraste d'une image et ainsi de lui redonner du peps ou de l'adoucir. Pour comprendre de manière intuitive le fonctionnement de ce traitement, étudions l'allure de l'histogramme pour des images peu ou trop contrastées :
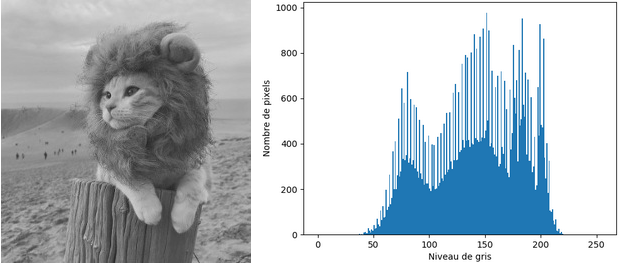
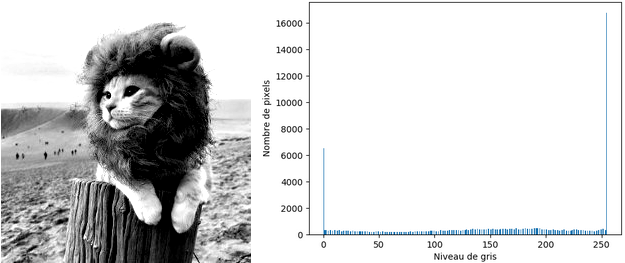
Comme vous pouvez le constater, les pixels des images dont le contraste est mauvais se répartissent dans tout l'intervalle disponible – donc un étirement d'histogramme n'améliorera rien – mais pas de manière équitable.
L'objectif est donc d'harmoniser la distribution des niveaux de gris de l'image, de sorte que chaque niveau de l'histogramme contienne idéalement le même nombre de pixels. Concrètement, on essaye d'aplatir au maximum l'histogramme original.
Pour cela, nous calculons d'abord l'histogramme cumulé normalisé de l'image, puis nous ajustons la valeur de chaque pixel en utilisant la formule mathématique suivante :
où désigne la probabilité qu'un pixel de l'image initiale soit d'intensité .
Pour mieux comprendre cette formule, rappelez-vous que le but est de répartir les niveaux de gris de l'image le plus équitablement possible sur . Autrement dit, nous voulons imposer la loi de probabilité comme étant uniforme discrète sur cet intervalle. Nous exploitons alors la loi de : sa fonction de répartition, donnée par , est multipliée par 255. Si l’on considère et comme des variables aléatoires continues, respectivement et , il est prouvé mathématiquement que est uniformément distribuée sur .
L'égalisation d'histogramme correspond à la fonction PIL.ImageOps.equalize . L'application de ce traitement sur l'image peu contrastée nous donne :
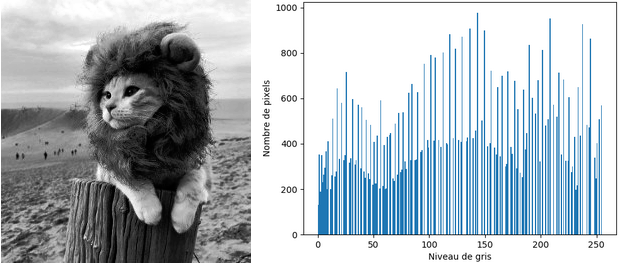
L'image est plus contrastée et son histogramme confirme que la distribution de ses niveaux de gris est plus uniforme.
Néanmoins, si l'histogramme de l'image corrigée n'est visiblement pas plat, l'histogramme cumulé normalisé montre que la fonction de répartition semble être linéaire comme celle de la loi uniforme :
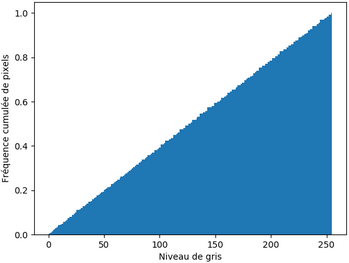
Transformations géométriques
Une autre catégorie de traitement ponctuel regroupe les transformations géométriques, qui modifient la position des pixels dans l'image. Une rotation, une translation ou un changement d'échelle (zoom) en sont des exemples typiques.
Une transformation géométrique est caractérisée par une matrice et un vecteur réels, respectivement notés et . Les nouvelles coordonnées du pixel de position initiale sont déterminées selon l'équation ci-dessous :
Plus précisément, les rotations, translations et zooms s'expriment de la manière suivante :
Translation de vecteur :
Zoom de coefficients et :
Rotation d'angle :
Rappelons qu'une image numérique est définie sur un ensemble discret : les coordonnées d'un pixel sont entières, de sorte que son intensité se trouve à la -ème ligne et -ème colonne de la matrice représentative.
Or, ces transformations, basées sur la géométrie euclidienne, sont définies dans un repère cartésien qui utilise des coordonnées réelles. Il s'agit donc d'une application qui va de dans ; par exemple, considérez une translation de vecteur . Afin de pouvoir représenter l'image numérique transformée, il est nécessaire d'arrondir les nouvelles coordonnées réelles vers les entiers les plus proches.
Cependant, ces arrondis ne garantissent pas un parcours de tous les pixels de l'image finale. Celle-ci risque alors de présenter des "trous", dus aux valeurs manquantes de sa matrice. Pour éviter ce problème, on utilise la transformation géométrique inverse, qui permet de passer de l'image transformée à l'image originale :
Le pixel de coordonnées dans l'image transformée prend ainsi la valeur du pixel de coordonnées dans l'image initiale.
Mais... Ne risque-t-on pas, encore une fois, d'obtenir des coordonnées réelles en sortie ?
Bien vu ! La transformation inverse nous assure une exploration de tous les pixels de l'image transformée, mais il s'agit à nouveau d'une application qui va de dans . Le problème n'est donc pas tout à fait résolu, puisque les coordonnées ne sont pas nécessairement entières !
Dans ce cas, comment déterminer l'intensité associée à un point de coordonnées réelles dans l'image originale ?
En fait, il faut coupler la transformation inverse avec une méthode d'interpolation, qui va associer à chaque couple de coordonnées dans l'image originale une valeur déterminée à partir des intensités des pixels voisins. Il existe deux modes d'interpolation principaux :
L'interpolation au plus proche voisin : la nouvelle valeur est déterminée comme l'intensité du pixel le plus proche. Il s'agit de la technique d'interpolation la plus simple et la plus rapide, mais en contrepartie, elle offre une moins bonne qualité visuelle
L'interpolation bilinéaire : la nouvelle valeur est calculée à partir des intensités des quatre pixels voisins
Comparons les effets des interpolations au plus proche voisin et bilinéaire avec une rotation (PIL.Image.rotate ) :

Vous pouvez constater que l'interpolation bilinéaire donne effectivement une image de bien meilleure qualité que l'interpolation au plus proche voisin.
Élimination du bruit
Enfin, la qualité d'une photo peut également être dégradée par du bruit numérique, c'est-à-dire par l'apparition aléatoire de "grains" superflus. Il s'agit d'un phénomène courant en photographie numérique, dû à un mauvais réglage de la sensibilité des capteurs de l'appareil photo, ou à une limitation de leurs capacités.
Le bruit peut être vu comme une image constituée de pixels dont les intensités ont été déterminées de manière aléatoire.
Une image étant définie soit comme une fonction soit comme une matrice, nous pouvons appliquer des opérations mathématiques usuelles, comme l'addition. Ainsi, on parle de bruit additif lorsque l'image bruitée est la somme de l'image originale et du bruit.
L'intensité du pixel de coordonnées dans l'image bruitée est alors donnée par la relation :
où , et désignent les intensités du pixel respectivement dans l'image bruitée, l'image originale et le bruit.
Un exemple très classique de bruit additif est le bruit gaussien, pour lequel les intensités sont choisies aléatoirement selon une loi normale : suit la loi . Plus la variance est élevée, plus le bruit est visible dans l'image.
Nous pouvons facilement générer du bruit gaussien dans une image. En Python, cela se fait avec la fonction numpy.random.normal, qui simule une variable aléatoire gaussienne :
# Charger l'image sous forme d'une matrice de pixels
img = np.array(Image.open('simba.png'))
# Générer le bruit gaussien de moyenne nulle et d'écart-type 7 (variance 49)
noise = np.random.normal(0, 7, img.shape)
# Créer l'image bruitée et l'afficher
noisy_img = Image.fromarray(img + noise).convert('L')
noisy_img.show()
Mais, l'image est devenue moins belle ! Comment est-ce qu'on se débarrasse du bruit ?
Plusieurs techniques de débruitage (ou lissage) ont été développées afin d'atténuer le bruit dans une image. Le lissage par moyennage désigne la solution la plus intuitive.
Ce qui rend l'image désagréable visuellement, c'est la présence de certains pixels qui ne semblent pas être en cohérence avec les autres éléments de la scène représentée : le bruit leur a donné des valeurs "aberrantes". Dans une image de bonne qualité, un pixel a généralement une intensité relativement similaire à celle de ses voisins.
Le lissage par moyennage consiste alors à remplacer la valeur de chaque pixel par l'intensité moyenne de son voisinage. Le voisinage est défini par une fenêtre carrée de taille impaire, centrée en le pixel à corriger. Le principe de cette méthode est schématisé ci-dessous :
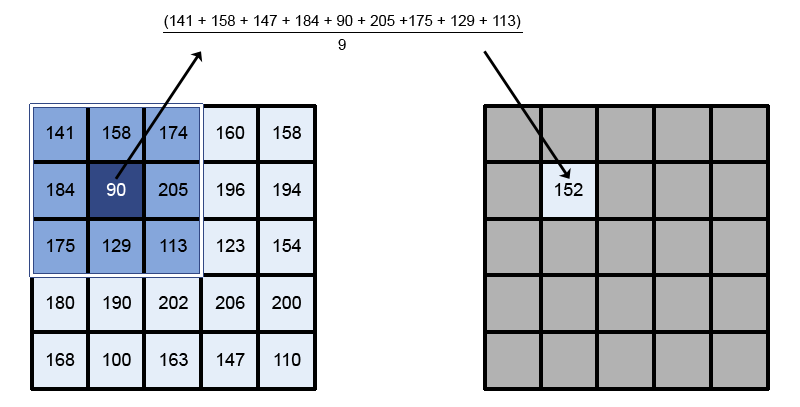
Comme la valeur de chaque pixel est modifiée en fonction des intensités de ses pixels voisins, il s'agit d'un traitement local.
En Pillow, le lissage par moyennage est implémenté dans la classe PIL.ImageFilter.BoxBlur et il s'applique avec la méthode PIL.Image.filter :
from PIL import ImageFilter
# Appliquer le lissage par moyennage (fenêtre de taille 9) et afficher le résultat
noisy_img.filter(ImageFilter.BoxBlur(1)).show()
Le bruit est bien atténué, mais en contrepartie, l'image est devenue floue – d'où l'appellation BoxBlur (blur = flou en anglais) dans Pillow !
Ok, mais pourquoi le lissage s'applique avec une méthode nommée filter ?
En réalité, le lissage par moyennage n'est qu'un exemple de filtre. Le chapitre suivant est consacré à cet outil fondamental en traitement d'images.
