Explorez vos données avec des algorithmes non supervisés

Nos données sont représentées sous la forme d'une matrice X de dimension   $\$\backslash (n\; \backslash times\; p\backslash )\$$   , où n est le nombre d'observations et p le nombre de variables les représentant. p est généralement un nombre assez grand, qui peut aller jusqu'à plusieurs dizaines de milliers dans certaines applications. C'est le cas par exemple lorsqu'on traite des images en haute résolution, et que chaque variable représente un pixel de cette image.

Dans cette partie, nous allons étudier des techniques non supervisées permettant de réduire ce nombre de variables. Il s'agira de trouver   $\$\backslash (m\backslash )\$$   variables, avec      , que nous allons choisir d'utiliser pour construire une nouvelle matrice   $\$\backslash (\backslash tilde\; X\backslash )\$$   , de dimension $\$\backslash (n\; \backslash times\; m\backslash )\$$  , pour représenter nos données.

Visualiser les données

Nous pouvons assez facilement représenter des données en 2 ou 3 dimensions. Mais au-delà, on est obligé de regarder les variables paire par paire (ou triplet par triplet). Ça devient assez vite difficile, voire impossible quand le nombre de dimensions augmente. Si l'on pouvait représenter nos données avec 2 ou 3 dimensions seulement, ce serait beaucoup plus simple !

Réduire les coûts

Si nous pouvons représenter nos données en quelques dimensions, cela fait aussi moins d'informations à stocker, ce qui réduit le coût en espace mémoire.

Par ailleurs, avoir moins de variables réduit la complexité des algorithmes d'apprentissage que nous pouvons utiliser, et donc les temps de calcul.

Enfin, si certaines variables sont inutiles, il n'est pas nécessaire de les obtenir pour de nouvelles observations : cela peut réduire le coût d'acquisition des données.

Améliorer la qualité des modèles d'apprentissage

En utilisant moins de variables, on peut construire des modèles avec moins de paramètres, donc plus simples, ce qui est généralement préférable pour éviter le surapprentissage.

De plus, les variables non pertinentes peuvent induire l'algorithme d'apprentissage en erreur. Prenons comme exemple l'algorithme des plus proches voisins, qui associe à une observation la même étiquette que celle de la majorité des k points d'entraînement les plus proches. Si l'on utilise la distance euclidienne, toutes les variables comptent autant dans le calcul des plus proches voisins. Mais si l'une de ces variables n'est pas pertinente, elle peut changer la définition du plus proche voisin, et introduire du bruit dans le modèle.

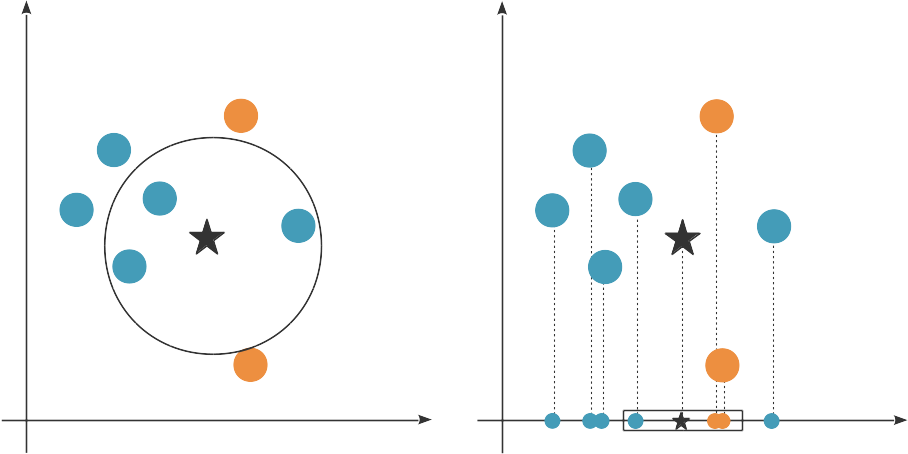
En utilisant les deux dimensions, les 3 plus proches voisins de l'étoile sont majoritairement bleus. En utilisant seulement la variable en abscisse, les 3 plus proches voisins sont majoritairement orange. Si la variable en ordonnée n'est pas pertinente, elle fausse l'algorithme.

Enfin, le fléau de la dimension (curse of dimensionality, en anglais) est le terme que nous utilisons pour qualifier le fait qu'il est très difficile de faire de l'apprentissage en haute dimension. En effet, en haute dimension, on a besoin de beaucoup plus de points pour couvrir tout l'espace. Voir aussi le chapitre correspondant dans le cours Initiez-vous au machine learning.

Une autre façon de présenter le fléau de la dimension est de dire que toutes les observations sont loin les unes des autres, et il est très difficile de trouver ce qu'elles peuvent avoir de commun ou de différent. Les méthodes ou intuitions qui marchent en petite dimension ne marchent pas nécessairement en grande dimension.

On en conclut que la réduction de dimension est nécessaire à la qualité de l'apprentissage.

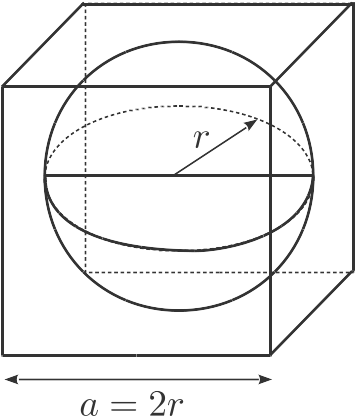
Pour comprendre pourquoi je dis que toutes les observations sont loin les unes des autres, on peut se placer en dimension p et regarder la proportion du volume d'un hypercube comprise à l'extérieur de l'hypersphère incrite dans cet hypercube.

En dimension 2, prenons un carré de côté a. Sa surface est   $\$\backslash (a^2\backslash )\$$   . Le disque inscrit dans ce carré a pour surface   $\$\backslash (\backslash pi\; \backslash frac\{a^2\}\{4\}\backslash )\$$   . La surface entre ce disque et le carré vaut donc $\$\backslash (a^2\; -\; \backslash pi\; \backslash frac\{a^2\}\{4\}\backslash )\$$   , et couvre donc une proportion $\$\backslash (\backslash frac\{a^2\; -\; \backslash pi\; \backslash frac\{a^2\}\{4\}\}\{a^2\}\; =\; 1\; -\; \backslash frac\{\backslash pi\}\{4\}\backslash )\$$  de la surface du carré.

En dimension p, prenons un hypercube de côté   $\$\backslash (a=2r\backslash )\$$   . Son volume est   $\$\backslash (2^p\; r^p\backslash )\$$   . Le volume d'une sphère de rayon r est donné par   $\$\backslash (\backslash frac\{2\; r^p\; \backslash pi^\{p/2\}\}\{p\; \backslash Gamma(p/2)\}\backslash )\$$   . Par conséquent, la proportion qui nous intéresse vaut :$\$\backslash (1\; -\; \backslash frac\{2\; r^p\; \backslash pi^\{p/2\}\}\{p\; \backslash Gamma(p/2)\; 2^p\; r^p\}\; =\; 1\; -\; \backslash frac\{\backslash pi^\{p/2\}\}\{p\; \backslash Gamma(p/2)\; 2^\{p-1\}\}\backslash )\$$   , qui tend vers 1 lorsque p tend vers l'infini.

Résumé

Réduire la dimensionalité des données, c'est-à-dire le nombre de variables utilisées pour les représenter, permet :

• de faciliter la visualisation des données ;

• de réduire les coûts de calcul, de stockage et d'acquisition des données ;

• d'améliorer l'apprentissage en construisant des modèles moins complexes, en éliminant les variables non pertinentes qui pourraient fausser les prédictions, et enfin en réduisant le problème du fléau de la dimensionalité.

Dans la suite de cette partie, nous allons voir des techniques linéaires de réduction de dimension non supervisées.