Commençons avec l'algorithme le plus célèbre en clustering : l'algorithme k-means, ou algorithme des centres mobiles en français.
Fonctionnement de l'algorithme
Vous allez voir, il est très intuitif et facile à comprendre.
Il faut tout d'abord déterminer combien de groupes on souhaite trouver : on appelle ce nombre .
L'objectif : trouver des groupes en faisant en sorte de minimiser l'inertie intraclasse.
L'algorithme du k-means travaille avec les centres de gravité des groupes. Seulement voilà, au départ, on ne connaît pas les groupes ! On ne peut donc pas connaître leur centre de gravité (que l'on appelle souvent un centroïde).
Mais ce n'est pas grave : on va supposer qu'on les connaît quand même, et les placer aléatoirement dans l'espace. Enfin... pas trop aléatoirement quand même : on va plutôt "piocher" au hasard des points qui font partie du nuage, pour y placer les centroïdes.
Une fois les centroïdes placés, on prend chaque point du nuage et on lui associe le cluster du centroïde dont il est le plus proche. On obtient donc un nuage de points dont chaque point appartient à l'un des K groupes.
Une fois cette opération faite, on calcule le centre de gravité de chaque groupe. Pour un groupe donné, le centre de gravité n'est généralement pas exactement au même endroit que là où l'on avait placé le centroïde initialement. On déplace donc ce centroïde sur le nouveau centre de gravité calculé.
Mais comme le centroïde a bougé, il faut recalculer, pour chacun des points du nuage, quel est le centroïde le plus proche, pour l'associer au bon cluster. Puis on recalcule le nouveau centre de gravité, et ainsi de suite... jusqu'à la convergence de l'algorithme.
Convergence ?
Ici, on dit que l'algorithme converge quand plus rien ne bouge d'une itération à l'autre, c'est-à-dire quand le centroïde reste immobile même après avoir recalculé pour chaque point son cluster.
Rien de tel qu'un petit schéma pour illustrer tout cela !
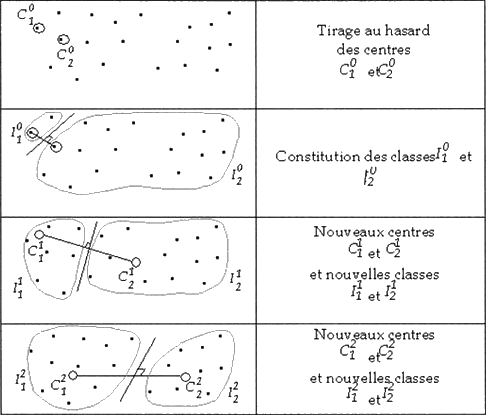
Avantages et inconvénients du k-means
L'algorithme du k-means converge en général très rapidement : il n'est pas rare qu'il atteigne la convergence au bout de 10 itérations, même avec beaucoup de points.
Cependant, il faut faire attention à un point. Avec votre échantillon, il y aura toujours (pour un nombre de clusters donné) une partition qui donnera une inertie intraclasse minimale, mais le k-means ne la trouvera pas toujours. En effet, cela dépend de l'initialisation des centroïdes : comme on les place aléatoirement, le résultat donné peut être différent quand on relance l'algorithme. Il est donc conseillé de relancer plusieurs fois l'algorithme pour sélectionner la partition dont l’inertie intraclasse sera la plus petite.
Les clusters choisis par le k-means sont aléatoires ?
Alors... oui et non. Ce qui est aléatoire, c'est le choix des premiers centroïdes. Du choix de ces centroïdes va dépendre les clusters retenus. Mais quand on a défini les centroïdes initiaux, il n'y a plus de place pour le hasard.
Malheureusement, le k-means n'est pas capable de déterminer le nombre de classes optimal : on est obligé de le lui spécifier au départ.
Si on lui demande de trouver 3 clusters alors que vos données sont très clairement regroupées en 5 clusters, alors le k-means vous donnera 3 clusters, même si ce n'est visiblement pas la solution la meilleure.
Il existe des algorithmes qui n'ont pas besoin qu'on fournisse explicitement le nombre de clusters à produire. Nous en verrons un exemple dans le chapitre suivant.
Cela peut être très utile, notamment s'il faut arriver à faire un partitionnement alors qu'on ne distingue pas facilement des clusters naturels.
C'est-à-dire ?
Pour bien comprendre, prenons des exemples... Supposons, tout d'abord, que nous avons ces données :
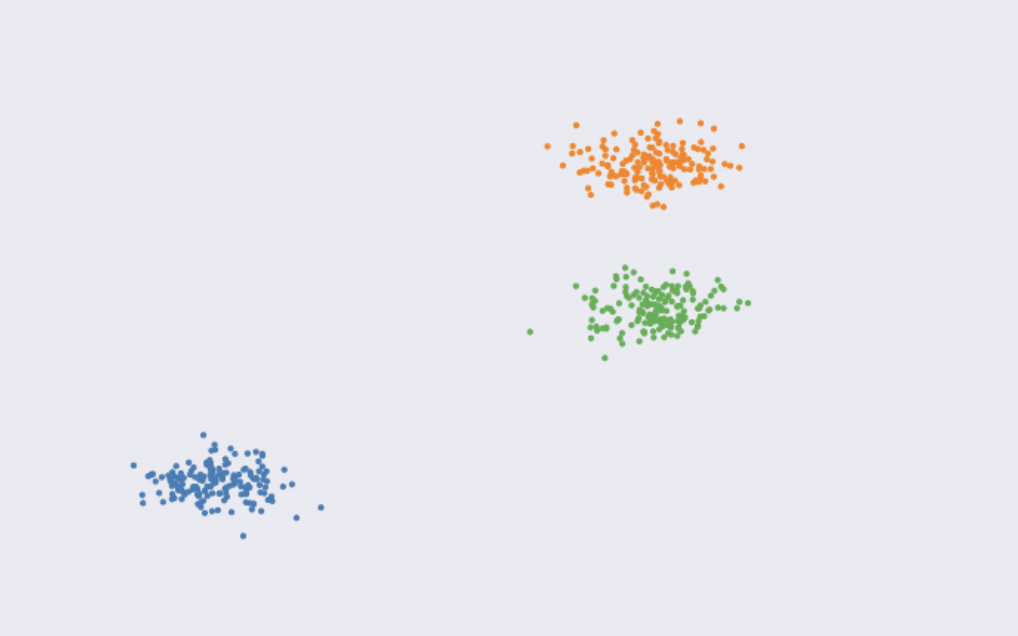
On voit à l'œil nu les clusters. Pas difficile de les déterminer !
Mais prenons un autre exemple :

Ici, il n'y a pas "vraiment" de clusters qui se dégagent. Une des propriétés du k-means, c'est justement d'être capable de forcer la clusterisation des données en fonction d'un nombre donné de clusters.
Voici ce que le k-means proposerait si on fixait un nombre de clusters à 3.
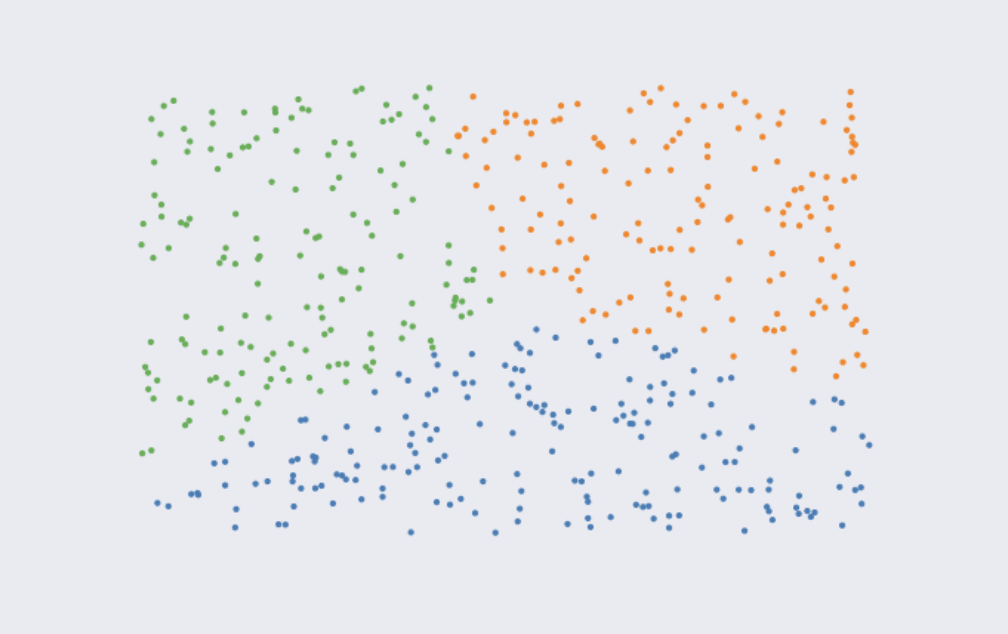
Alors, certes, la clusterisation n'est pas qualitative, les clusters changeraient beaucoup si on relançait l'algorithme. Mais du moment qu'on lui donne un nombre de clusters défini, le k-means sait créer le bon nombre de partitions.
Quel intérêt de forcer le partionnement des données ?
Il pourra arriver des configurations ou, soit les données sont très difficiles à partitionner, soit les clusters sont difficiles à interpréter. Dans les deux cas, et dans bien d'autres, le k-means sera un algorithme très utile !
Le nombre de clusters
Pour choisir le nombre optimal de clusters, on lance souvent le k-means plusieurs fois, avec différentes valeurs de . Pour chacune d'entre elles, on note l’inertie intraclasse obtenue.
Plus il y a de clusters, plus le nombre d'individus par cluster diminue, et plus les clusters sont resserrés. Donc, bien entendu, l’inertie intraclasse diminue forcément quand K augmente !
Pour déterminer le nombre de clusters à étudier, on s'intéresse au graphique qui trace l'inertie intraclasse en fonction du nombre de clusters. On cherche plus particulièrement une "cassure" dans la courbe. Cette "cassure" nous indique à partir de quel nombre de clusters nous "allons trop loin".
Dans la pratique, cela donne un graphique comme celui-là :
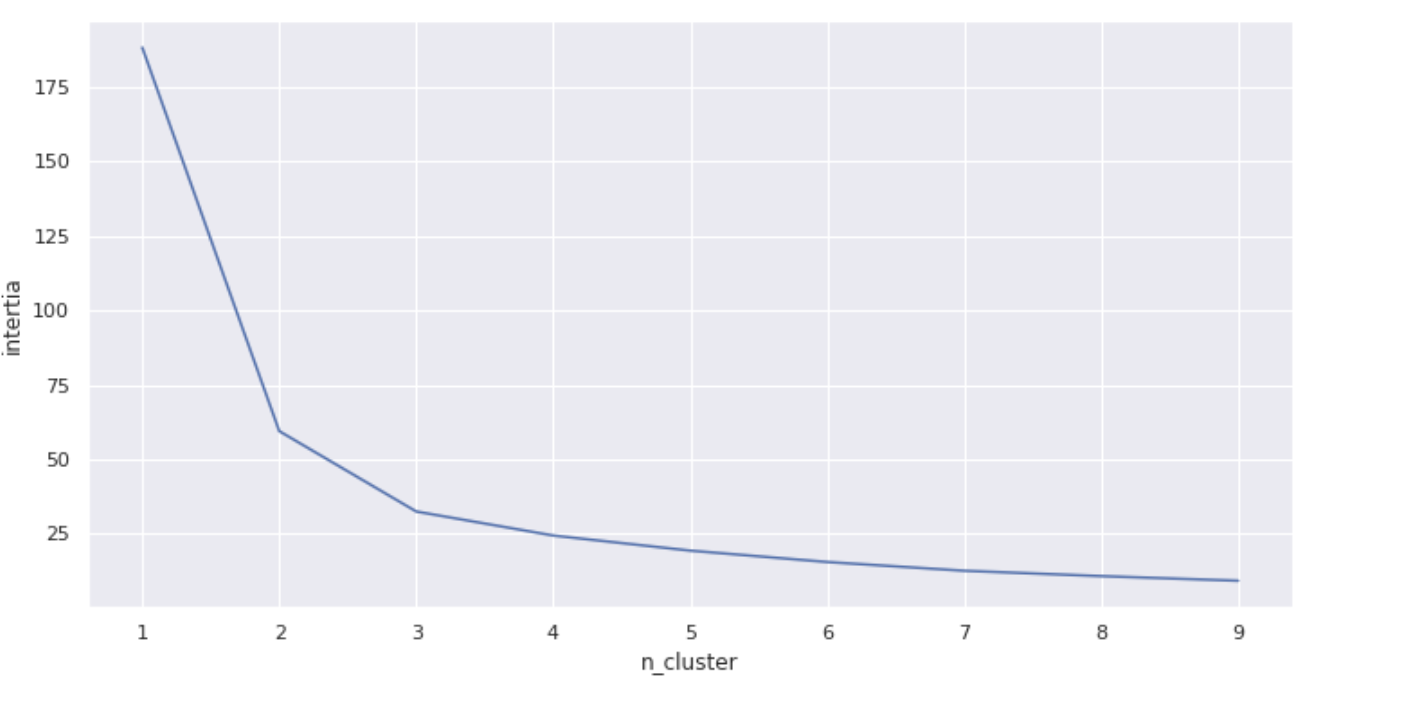
Dans les faits, on pourrait retenir un nombre de clusters à 2, voire à 3. Alors comment faire ?
Peut-être pourrait-on relancer notre algorithme plusieurs fois ?
Malheureusement cela ne fonctionnera pas. Même si les clusters pourront légèrement changer, il y a de grandes chances que votre graphique ait la même forme.
Alors comment faire?
Eh bien nous avons 2 solutions :
La première, la plus simple, consiste à choisir le nombre de clusters pour lequel nous considérons que la cassure est la dernière qui est "forte", ici on dirait 3.
La deuxième, plus complexe, est de prendre le nombre de clusters de la première solution et de garder ce nombre, le nombre inférieur et celui supérieur. Ici on retiendrait donc 2, 3 et 4. Il conviendra d'analyser les différents clusters obtenus, et de retenir celui que nous jugerons le plus pertinent par la suite.
En pratique
Commençons par importer nos librairies :
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.cluster import KMeans
Chargeons ensuite nos données. Nous prendrons le jeu de données de fleurs d'iris fourni par scikit-learn :
# On charge le dataset iris :
iris = datasets.load_iris()
# On extrait X :
X = iris.data
# On peut le transformer en DataFrame :
X = pd.DataFrame(X)
# Cela permet d'appliquer la méthode .head :
X.head()Ensuite pour chaque nombre de clusters, on entraîne un k-means, et on enregistre la valeur de l'inertie :
# Une liste vide pour enregistrer les inerties :
intertia_list = [ ]
# Notre liste de nombres de clusters :
k_list = range(1, 10)
# Pour chaque nombre de clusters :
for k in k_list :
# On instancie un k-means pour k clusters
kmeans = KMeans(n_clusters=k)
# On entraine
kmeans.fit(X)
# On enregistre l'inertie obtenue :
intertia_list.append(kmeans.inertia_)On peut ensuite faire un graphique pour constater la "cassure" dans la courbe. On affiche en x le nombre de clusters, la variable k_list et en y la liste des inerties intraclasses, la variable inertia :
fig, ax = plt.subplots(1,1,figsize=(12,6))
ax.set_ylabel("intertia")
ax.set_xlabel("n_cluster")
ax = plt.plot(k_list, intertia_list)Allez plus loin
Pour ceux qui souhaitent aller plus loin, je vous invite à regarder ce notebook.
Pour les autres, rassurez-vous, nous verrons tout cela dans le TP !
En résumé
L'algorithme du k-means est un algorithme très utilisé en clustering.
Il fonctionne généralement bien, il est rapide et relativement simple à comprendre.
Il est non déterministe, c'est-à-dire que les clusters obtenus peuvent changer légèrement si on relance l'algorithme plusieurs fois.
Il a toutefois besoin qu'on lui spécifie le nombre de clusters à produire.
Pour choisir le nombre de clusters, on applique la méthode du "coude", et on cherche une "cassure" dans la courbe liant la variance intraclasse au nombre de clusters.
Passons maintenant à autre chose : comment effectuer une classification hiérarchique !
