Maintenant que nous avons compris le principe de l’ACP, passons au concret !
Nous avons 2 objectifs. Pour chacun d’eux, nous allons utiliser un espace différent, ainsi qu’un type de graphique différent.
Répondre au premier objectif par le nuage des individus
Nous avons déjà parlé du nuage des individus précédemment : vous le connaissez donc déjà.
Pour rappel, si notre échantillon a variables quantitatives, alors on se place dans un espace à dimensions, et nous plaçons les individus dans cet espace. Chaque individu est représenté par un point.
Il est noté grand car il peut comporter des nombres réels, c'est-à-dire tous types de nombres que nous connaissons : 1, 0.5, -12.3 et même des fractions comme 1/3, et petit car il a p dimensions.
On a donc un espace à dimensions qui contient individus.
Pour placer les points, il s’agit de considérer que chaque colonne de notre échantillon correspond à une dimension, et de placer les individus en fonction de leurs coordonnées dans .
Pour répondre à l’objectif numéro 1 (étudier la variabilité des individus), on recherche les axes d’inertie maximum, comme expliqué au chapitre précédent.
Cela étant dit, continuons...
Répondre au second objectif par le nuage des variables
Pour le second objectif, nous nous plaçons dans un espace totalement différent !
Pour l’objectif 1, chaque colonne de l’échantillon correspondait à une dimension de l’espace, et chaque ligne (chaque individu) correspondait à un point dans cet espace. Mais ici, c’est l’inverse :waw: !!!
Chaque ligne correspondra à une dimension, et chaque colonne à un point ! On est donc dans un espace totalement différent ! Celui-ci aura donc autant de dimensions que d’individus, ; et autant de points que de variables, .
L'espace
Nous avons donc :
, le nuage des variables ;
et , l'espace à dimensions dans lequel il est placé.
Voici un petit exemple avec un échantillon de 3 individus et 4 variables. Les individus sont des cours OpenClassrooms :
| Dernière mise à jour | Moyenne de classe | Nombre de chapitres | Difficulté |
Cours SQL | 20 jours | 85 % | 28 | 2 |
Cours Python | 40 jours | 83 % | 10 | 3 |
Cours HTML | 60 jours | 80 % | 19 | 1 |
Comme nous l’avons évoqué au chapitre précédent, nous centrons puis réduisons les données, ce qui nous donne ce nouveau tableau (qui n’a plus d’unités à la suite de la réduction) :
| Dernière mise à jour | Moyenne de classe | Nombre de chapitres | Difficulté |
Cours SQL | -1.225 | 1.136 | 1.225 | 0 |
Cours Python | 0 | 0.162 | -1.225 | 1.225 |
Cours HTML | 1.225 | -1.300 | 0 | -1.225 |
Avec ce tableau, nous aurons 4 points en 3 dimensions :
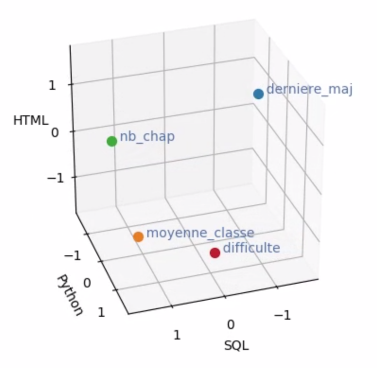
Représenter le nuage de variables dans cet espace apporte certains avantages très intéressants.
Tout d’abord, si l'on prend deux points (correspondant donc à 2 variables et ), et que l’on calcule l’angle (où O est l'origine du repère), alors cet angle est lié au coefficient de corrélation des variables et !
C’est pour cette raison que l’on préfère représenter les points par des flèches : il est plus simple visuellement de regarder un angle entre deux flèches.
C’est une aubaine ! On souhaitait justement étudier les liaisons entre les variables : ici, elles sont tout simplement représentées par les angles entre les flèches !
Ensuite, si les données sont centrées et réduites, les longueurs de toutes les flèches sont égales ! On peut même connaître cette longueur : c’est , la racine carrée du nombre d’individus dans notre échantillon.
Comme toutes nos flèches sont de longueur égale, et qu'elles partent toutes de l'origine, alors leurs extrémités sont toutes situées sur une même hypersphère de rayon . C'est pour cela que, dans l'illustration ci-dessus, j'ai représenté les 4 flèches dans une sphère.
Les axes principaux d'inertie du nuage des variables
Imaginons un échantillon dans lequel chaque individu est décrit par 15 variables. Ces 15 variables sont regroupables en 2 groupes : un groupe de 10 variables et un autre de 5 variables. Les 10 premières sont très corrélées entre elles, et les 5 restantes sont également corrélées entre elles, mais ne sont pas corrélées aux 10 premières.
Quand on représente le nuage de ces 15 variables, nous avons 15 flèches.
On aura donc 10 flèches séparées par un angle très petit. Autrement dit, ces 10 flèches pointent à peu près dans la même direction. Quant aux 5 autres variables, leurs 5 flèches pointeront aussi à peu près dans la même direction, mais cette direction sera différente du groupe des 10 flèches précédentes.
Imaginons que nous construisions une maquette en 3D. Cette maquette représentera le nuage des variables d'un échantillon composé de 3 individus décrits par 15 variables.
Sur celle-ci, vous représentez ces 15 variables par 15 flèches de bois. Si vous étudiez l’équilibre de cette maquette, vous vous rendez compte que les 10 bouts de bois qui pointent dans la même direction déséquilibrent la maquette dans une certaine direction. Autrement dit, ils créent une inertie dans une certaine direction. La direction d’inertie maximale est donnée par ces 10 bâtons ; il y aura également une autre direction d’inertie secondaire induite par les 5 autres bâtons.
On en revient ici aussi au concept de direction d’inertie maximale, comme quand nous parlions du nuage des individus !
Un résultat remarquable
Attention, vous allez être bluffé !
Nous avons ici 2 espaces totalement différents : et . Le premier est à dimensions et contient le nuage d’individus , et l’autre est à dimensions et contient le nuage des variables .
Dans chacun des 2 espaces, on a cherché les axes principaux d’inertie.
Dans , nous avons vu que l’on pouvait considérer les axes principaux comme de nouvelles variables calculables à partir des variables initiales.
Eh bien, figurez-vous que, si l'on place ces nouvelles variables dans , alors celles-ci coïncident exactement avec les axes principaux d’inertie du nuage des variables !
Dit comme cela, ça n'est peut-être pas très clair. Mais on peut le dire autrement...
Étudier les axes d’inertie des individus est équivalent à étudier les axes principaux d’inertie des variables !
En résumé
Nous avons 2 objectifs principaux lors d'une ACP : étudier la variabilité des individus et le lien entre les variables
Pour ce faire, on peut travailler sur la projection des dimensions en fonction des individus.
Cette projection peut se faire à l'aide de points, mais on peut aussi considérer chaque dimension comme un vecteur.
La notion essentielle dans ce travail est celle d'inertie ; en effet, on cherche à maximiser la variance de nos données au travers de ces nouvelles dimensions.
Magie des magies, nos deux objectifs sont en quelque sorte le même.
Allez plus loin : Calcul des composantes principales du nuage , valeurs propres et vecteurs propres
Notons , un vecteur unitaire de l'axe de rang . Pour le moment, nous ne connaissons pas encore les composantes de : c'est ce que nous allons chercher ici.
On peut ranger les projections dans le vecteur , et comme s'obtient par produit scalaire entre et la i-ième ligne de nos données, on peut alors écrire sous forme matricielle :
La quantité à maximiser (donnée dans l'encadré ci-dessus) peut donc être écrite sous cette forme matricielle :
Maximiser la quantité signifie trouver quel rend cette quantité maximale. En replongeant dans vos souvenirs d'algèbre linéaire, vous verrez que l'on résout ce type de problème par une diagonalisation de matrice.
On peut montrer mathématiquement (nous ne le ferons pas ici, mais vous pouvez consulter la démonstration ici) que le vecteur u_s vérifie :
À partir de ce résultat, on voit que est le vecteur propre unitaire associé à la valeur propre de la matrice , les valeurs propres étant rangées dans l'ordre décroissant sur la diagonale.
De plus, on voit que est égal à l'inertie portée par l'axe (c'est l'inertie de la projection du nuage des individus sur ).
(Source : Analyse factorielle multiple avec R, Jérôme Pagès, éditions EDP Sciences.)
