Réalisez des calculs distribués sur des données massives

Dans le chapitre précédent, nous avons découvert le cadre de programmation MapReduce qui vise à proposer une stratégie générique pour paralléliser les traitements, quel que soit le problème cible. Cette stratégie doit se faire uniquement à l'aide des deux opérateurs MAP et REDUCE et nous avons vu aussi qu'il est nécessaire de structurer les données en paires(clé, valeur).

Dans l'exemple WordCount, c'est assez intuitif et donc rapide ! Pour autant, pour un problème donné, il n’est pas toujours évident de le reformuler selon ce cadre. C’est d’ailleurs même parfois impossible.

Pour vous familiariser un peu plus avec la logique du cadre MapReduce, nous allons l’appliquer à deux problèmes très différents :

• la multiplication d’une matrice par un vecteur, nécessaire entre autres, pour le calcul du PageRank, le fameux algorithme de pondération d’une page web, à l'origine du succès de Google.

• le problème de la jointure de deux tables de données, qui est un problème très classique mais très coûteux.

Exemple 1 : Multiplication d'une matrice par un vecteur

Le premier problème auquel nous allons nous intéresser est celui qui consister à multiplier une matriceAde grande taille (n×n) par un vecteurvde taillen. Il s'agit donc de calculer

$\$\backslash [Av\; =\; x\backslash ]\$$

avec

$\$\backslash [x\; =\; (x\_1,...,x\_n)\backslash ]\$$

et

$\$\backslash [x\_i\; =\; \backslash sum\_\{j=1\}^\{n\}\; a\_\{ij\}v\_j\backslash ]\$$

Vous êtes peut-être en train de vous dire que c'est un joli problème mathématique mais bien loin de vos préoccupations ! Et bien en fait, pas tant que cela ! Sachez tout d'abord que c'est en grande partie pour ce problème que MapReduce a été conçu chez Google car c'est une opération nécessaire au calcul du fameux PageRank, utilisé pour ordonnancer les résultats d'une recherche Web. Dans ce cas, $\$\backslash (n\backslash )\$$ est le nombre de pages web indexées... oui, un vrai problème big data ! De plus, c'est une opération très commune, que l'on retrouve dans de nombreux problème et notamment dans les algorithmes du data scientist.

Pour ce problème, la vraie question est la manière dont nous allons représenter la matrice $\$\backslash (A\backslash )\$$ et donc la forme de l'entrée donnée à MapReduce. Très souvent, pour ce type de problèmes, nous sommes en présence de matrices creuses et on évite donc de réprésenter les zéros. Ici, nous allons donc considérer que la matrice $\$\backslash (A\backslash )\$$ est stockée sous la forme de triplets  $\$\backslash ((i,\; j,\; a\_\{ij\})\backslash )\$$ (les coordonnées sont explicites). De même, le vecteur $\$\backslash (v\backslash )\$$ est stocké sous la forme de paires $\$\backslash ((j,\; v\_j)\backslash )\$$ . Vous allez voir que nous avons presque répondu au problème en choisissant cette représentation.

L'autre difficulté pour ce problème est la taille du vecteur $\$\backslash (v\backslash )\$$ . En particulier, deux cas vont devoir être considérés selon la taille de ce vecteur $\$\backslash (v\backslash )\$$ .

Cas 1 : vest suffisamment petit pour tenir dans la mémoire du nœud MAP.

Dans ce cas, l'opération MAP peut être relativement simple à écrire si on considère qu'elle prend en entrée le vecter $\$\backslash (v\backslash )\$$ en entier et un élément non vide de la matrice, c'est-à-dire un triplet $\$\backslash ((i,\; j,\; a\_\{ij\})\backslash )\$$ . En effet, pour chaque élément de la matrice, l'opération MAP va juste générer la paire $\$\backslash ((i,\; a\_\{ij\}v\_j)\backslash )\$$ . On a donc choisi de prendre comme clé pour MAP, un numéro correspondant à une ligne de la matrice. C'est plutôt logique si on se rapporte à la formule ci-dessus car on somme sur les lignes.

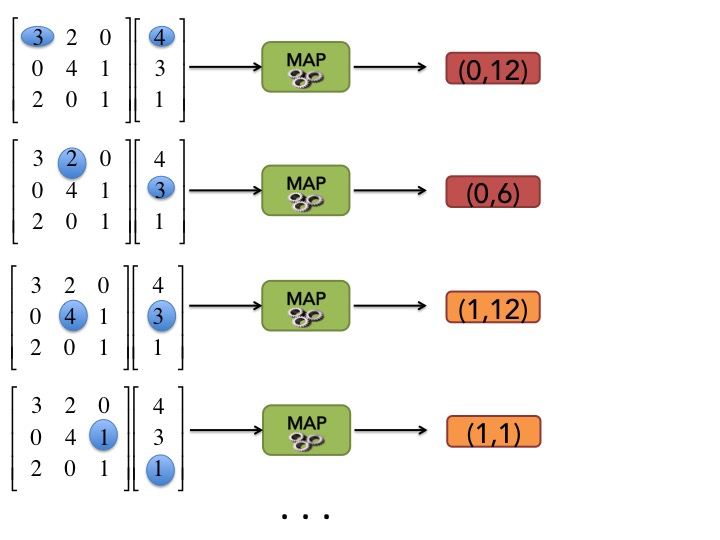
Comme pour WordCount, nous pouvons utiliser notre baguette magique et l'opération SHUFFLE  and SORT regroupe toutes les valeurs associées à la même clé $\$\backslash (i\backslash )\$$ dans une paire $\$\backslash ((i,\; [a\_\{i1\}v\_1,\; ...,\; a\_\{in\}v\_n])\backslash )\$$ .

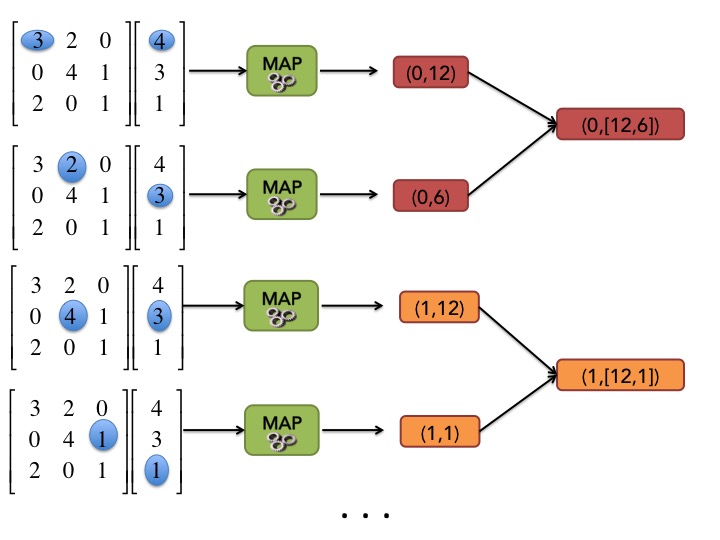
L'opération REDUCE est donc aussi très évidente, il suffit de faire la somme de toutes les valeurs associées à une clé donnée.

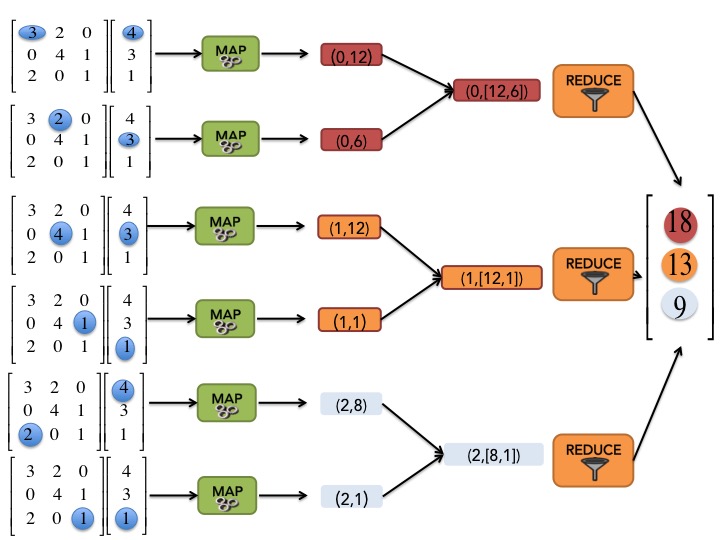
Cas 2 : v est trop grand pour tenir dans la mémoire du nœud MAP.

Étudions maintenant le cas où le vecteur $\$\backslash (v\backslash )\$$ est trop gros pour tenir entièrement en mémoire des nœuds MAP. Il faut alors ici appliquer le principe de diviser pour régner. Il faut découper le vecteur $\$\backslash (v\backslash )\$$ en bandes horizontales (qui tiennent en mémoire) et faire de même mais verticalement pour la matrice $\$\backslash (A\backslash )\$$ . Le problème initial est ainsi découpé en sous-tâches et on assigne à chaque nœud MAP un morceau de la matrice et la bande de vecteur correspondante.

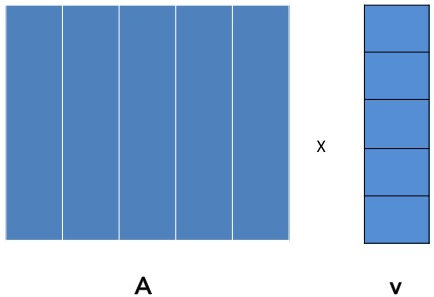
On peut alors appliquer la même stratégie pour les fonctionsmapetreduceque précedemment.

Exemple 2 : Jointure de deux tables de données

Passons maintenant à un exemple tout différent. Nous allons supposer que vous venez d'être recruté·e par une entreprise qui vend en ligne des films en flux continu sur Internet (oui... un marché pour lequel il y a une belle concurrence !). Cette entreprise se démarque des autres par son gigantesque catalogue de films. Par contre, elle propose uniquement de naviguer dans son catalogue et n'a pas su mettre en place un outil de recherche de films dans son catalogue. Par exemple, il est impossible pour les utilisateurs de faire une recherche sur l'ensemble des films réalisés par un réalisateur donné. C'est justement la première mission que vous donne votre responsable. Il vous fournit deux tables de données, une table des réalisateurs dans laquelle chaque réalisateur est associé à un unique identifiant et une table des films avec pour chaque film, les informations le concernant dont l'identifiant de son réalisateur.

À première vue, cela semble assez simple. Il suffit de faire une jointure entre la table des films et la table des réalisateurs en concaténant tous les films et les réalisateurs dont l'identifiant réalisateur coïncide :

SELECT *
FROM Films F JOIN Realisateurs R
ON F.ID_realisateur=R.ID_realisateur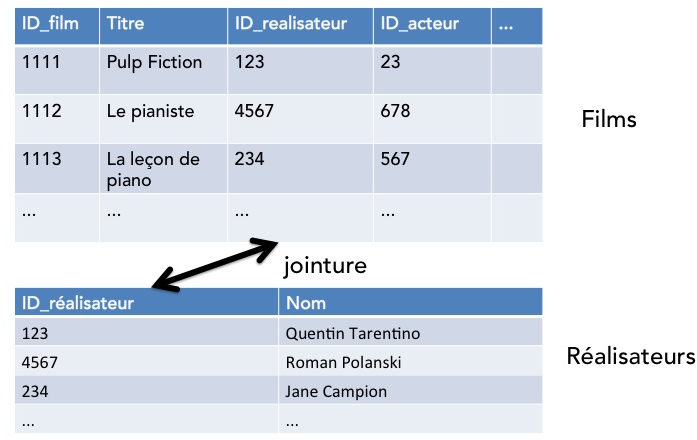

Oui, mais en grande dimension ? Ici, vous avez trop de données pour pouvoir faire cette opération de jointure de la sorte et une solution est donc de faire cette jointure de manière distribuée avec MapReduce.

Ici, nous allons appliquer une stratégie qui s'appelle Reduce-Side Join, c'est-à-dire que l'opération de jointure en tant que telle sera effectuée dans la phase REDUCE.

Avant de commencer et pour rendre plus facile l'explication, nous allons simplifier la table des films en mettant le champ correspondant à la clé de jointure en premier et en ne gardant comme information que le nom du film. Ce n'est bien evidemment pas nécessaire en vrai. On va donc dans la suite faire comme si nous travaillions avec les deux tables suivantes :

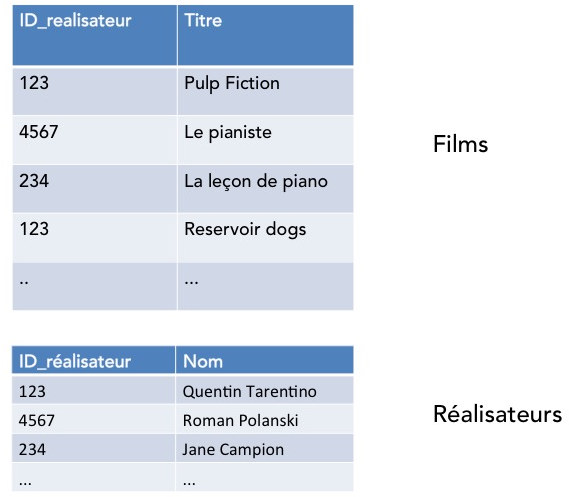
Avant de nous intéresser aux opérations MAP et REDUCE, nous allons aussi regrouper les enregistrements des deux tables en une seule longue liste d'enregistrements en ajoutant à chaque enregistrement le nom de la table dont il est issu. Pour notre problème, on obtiendrait donc une liste d'enregistrements comme ci-dessous.

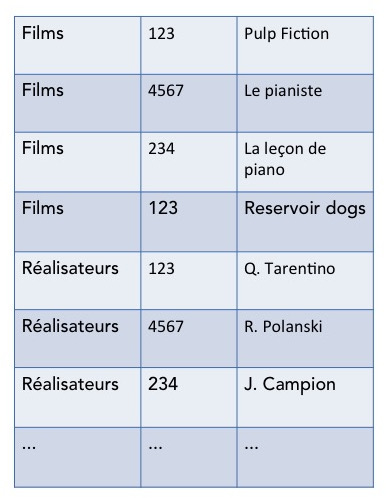
L'opération MAP est donc ensuite facile à concevoir. Il suffit de renvoyer pour chaque enregistrement la paire(clé, valeur)où la clé est la clé de jointure (ID_realisateur) et la valeur est le contenu de l'enregistrement.

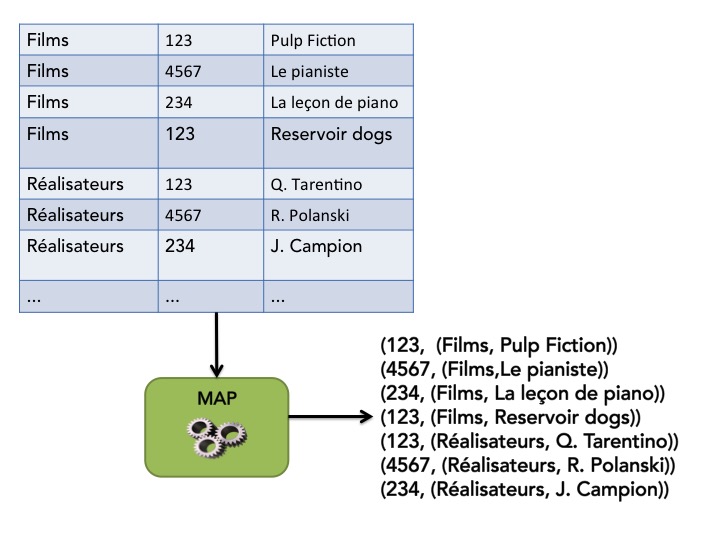
Comme pour WordCount, on va supposer que les données d'entrée sont structurées en paires(clé, valeur)avec comme clé le nom du fichier et comme valeur une liste d'enregistrements de type<String, Int, String>.

Et on peut donc écrire très facilement un code correspondant à l'opération MAP pour ce problème de jointure :

def map(key,value):
    intermediate = []
    for i in value:
        intermediate.append((i[1], (i[0], i[1:])))
    return intermediate

Nous appliquons maintenant notre petit coup de baguette magiqueSHUFFLE and SORTet les résultats intermédiaires sont alors regroupés par clé de jointure commune et chaque paire regroupée constitue donc une entrée idéale à une opération REDUCE.

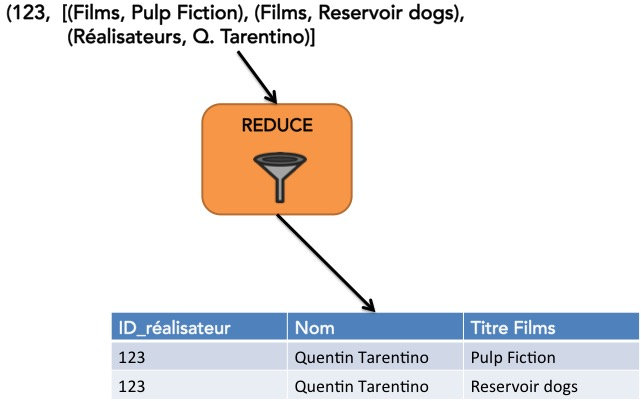
L'opération REDUCE est aussi facile à concevoir. Elle concatène les enregistrements des tables Films et Réalisateurs associées à une même clé de jointure. Et au final, nous avons donc le schéma d'exécution suivant de MapReduce pour notre problème de jointure :

Nous venons donc de voir au travers de deux exemples comment concevoir des algorithmes MapReduce en suivant le processus suivant :

1. Choisir une manière de découper les données afin que l'opération MAP soit parallélisable.

2. Choisir la clé à utiliser pour le problème ciblé.

3. Ecrire le code de la fonction pour l'opération MAP.

4. Ecrire le code de la fonction pour l'opération REDUCE.

En résumé

• MapReduce est bien un modèle et un cadre générique pour la parallélisation de traitements. Nous venons en effet de voir qu'il peut s'appliquer de manière identique sur des problèmes de nature relativement différente.

• Souvent, ce ne sont pas les opérations MAP et REDUCE qui sont les plus difficiles à concevoir mais la manière de représenter les données pour permettre d'appliquer facilement le modèle.

• C'est par la pratique que l'on acquière cette méthodologie.