Maintenant que nous avons un jeu de données bien propre, nous pouvons nous concentrer un peu plus sur l'analyse de nos variables. Une des premières questions qui viendraient serait alors : comment peut-on représenter une variable ?
Jusqu'à maintenant, nous avons vu comment afficher un échantillon de transactions bancaires (sous forme de tableau où chaque ligne représente un individu, et chaque colonne une variable). Pour représenter la variable categ par exemple, on pourrait sélectionner la colonne categ du tableau, et l'afficher telle quelle :
Mais il faut avouer que c'est assez illisible ! :waw: En plus, il est fréquent d'avoir des échantillons de 1 000 individus ou plus. Une colonne avec 1 000 valeurs dedans, c'est très moche et très difficile à interpréter. Il y a une solution bien meilleure, qui consiste à dire :
Il y a 39 fois la valeur COURSES, 212 fois la valeur AUTRE, 21 fois la valeur TRANSPORT, etc.
Cette formulation est appelée distribution empirique. C'est cette distribution que l'on se propose de représenter graphiquement ici.
Représentez une distribution empirique
Les différentes "possibilités" que l'on peut observer pour la variable categ sont ses modalités. Les modalités de la variable categ sont : courses, transport, autre, loyer, etc. Pour une variable quantitative cependant, on les appelle les valeurs possibles. On associe à chaque modalité (ou valeur) un effectif. L'effectif de la modalité courses est .
En divisant un effectif par le nombre d'individus de l'échantillon (noté ), on obtient une fréquence.
La distribution empirique d'une variable, c'est l’ensemble des valeurs (ou modalités) prises par cette variable, ainsi que leurs effectifs associés. On trouve aussi une autre version : l’ensemble des valeurs (ou modalités) prises par cette variable, ainsi que leurs fréquences associées. On peut présenter ceci sous forme de tableau. Nous approfondirons cette présentation dans le chapitre suivant :

Passons maintenant aux représentations graphiques.
Cas des variables qualitatives
Voici 2 représentations possibles de la distribution de la variable categ :

À gauche, vous avez le diagramme en secteurs, plus connu sous le nom de diagramme en camembert. Si les francophones y voient un camembert (fleuron de la gastronomie française), les anglophones y voient plutôt une tarte, et l'appellent donc pie chart. Ici, l'angle de chaque secteur est proportionnel à l'effectif de chaque modalité.
À droite, c'est le diagramme en tuyaux d'orgue, appelé en anglais bar chart. La hauteur des tuyaux est égale à l'effectif de chaque modalité, ou bien (au choix) égale à la fréquence de chaque modalité, comme c'est le cas ici.
Le code ayant généré les deux graphiques ci-dessus est le suivant :
# Diagramme en secteurs
data["categ"].value_counts(normalize=True).plot(kind='pie')
# Cette ligne assure que le pie chart est un cercle plutôt qu'une éllipse
plt.axis('equal')
plt.show() # Affiche le graphique
# Diagramme en tuyaux d'orgues
data["categ"].value_counts(normalize=True).plot(kind='bar')
plt.show()Ici, nous reprenons le même raisonnement qu'au début de ce chapitre. On commence par sélectionner la colonne souhaitée data['categ'] , puis on compte le nombre d'apparitions de chaque modalité : data['categ'].value_counts() .
Pour obtenir les fréquences, on peut éventuellement ajouter normalize=True. On obtient donc la distribution empirique. Pour l'afficher, on fait appel à la méthode plot, à laquelle on spécifie le type de graphique souhaité ( pie ou bar ).
Si la variable est qualitative ordinale, alors il suffit de classer sur le graphique les modalités en ordre croissant.
Cas des variables quantitatives
Variables discrètes
Pour les variables discrètes, on les représente par un équivalent du diagramme en tuyaux d'orgue : le diagramme en bâtons. Cependant, avec les variables qualitatives, on pouvait placer les tuyaux un peu n'importe où sur l'axe horizontal. Mais avec une variable quantitative, on est contraint à placer précisément les bâtons sur l'axe horizontal. Comme on doit être précis, on préfère que les bâtons soient très fins.
Pour représenter cela, nous allons créer une variable quart_mois pouvant prendre les valeurs 1, 2, 3 ou 4, et indiquant l'avancée dans le mois (1 : début, ..., 4 : fin de mois) :
data['quart_mois'] = [int((jour-1)*4/31)+1 for jour in data["date_operation"].dt.day]On peut à présent représenter sa distribution :
# Diagramme en bâtons
data["quart_mois"].value_counts(normalize=True).plot(kind='bar',width=0.1)
plt.show()
Variables continues
Prenons l'exemple de la taille d'une personne : c'est une variable continue. On peut très bien avoir une personne de taille 1,47801 m et une autre de 1,47802 m. Ces deux tailles sont différentes : faut-il alors afficher sur notre graphique 2 bâtons, un pour chacune des 2 tailles ?
Tu chipotes, 1,47801 m et 1,47802 m, c'est quasiment la même valeur, il faut donc que tu les considères comme égales !
Tout à fait ! Considérer que 1,47801 m et 1,47802 m sont presque égales, c'est regrouper ces valeurs. On dit alors que l'on agrège des valeurs en classes. Si on décide d'agréger en classes de taille 0,2 m, alors ces 2 valeurs seront toutes les deux situées dans la classe .
Le fait d'agréger une variable s'appelle la discrétisation (en anglais : binning, bucketing ou discretization).
Ainsi, pour les variables continues, on utilise l'histogramme, dans lequel les valeurs sont agrégées. Ici, comme on représente des classes (ou des intervalles, si vous préférez), on n'utilise plus de fins bâtons, mais des rectangles dont la largeur correspond à la largeur de la classe.
# Histogramme
data["montant"].hist(density=True)
plt.show()
# Histogramme plus beau
data[data.montant.abs() < 100]["montant"].hist(density=True,bins=20)
plt.show()
On souhaite regrouper les valeurs en classes. Utiliser value_counts() n'aurait donc pas vraiment de sens : on utilise donc la méthode hist(), qui s'occupe elle-même de regrouper les valeurs en classes.
Le premier histogramme généré est un peu trop étalé, car il y a des montants très grands et très petits. On filtre donc ici les montants compris entre -100 € et 100 € grâce à data[data.montant.abs() < 100] (on utilise pour cela la valeur absolue). Enfin, on peut aussi spécifier le nombre de classes voulues grâce au mot clé bins : ici 20.
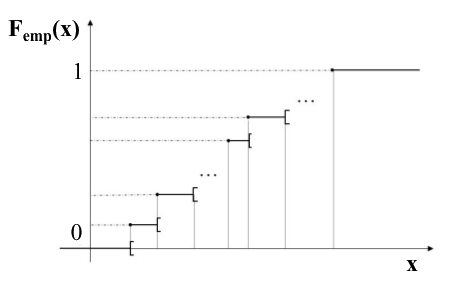
Si cependant, vous ne souhaitez pas agréger les valeurs, il existe une autre solution : représenter la fonction de répartition empirique. Il faut vous la représenter comme un escalier. Pour la représenter, on parcourt l'axe horizontal, des petites valeurs vers les grandes valeurs. À chaque fois que l'on rencontre une valeur qui est présente dans notre échantillon, on monte d'une marche. Il y aura donc autant de marches que de valeurs, et d'ailleurs autant que d'individus. Toutes les marches ont la même hauteur.
Une fois parcouru toutes les valeurs de l'échantillon, on aura atteint le haut de l'escalier. On dit (arbitrairement) que le haut de l'escalier est d'une hauteur de 1.
En résumé
Le calcul de la distribution empirique est la première étape pour la représentation graphique d'une variable qualitative.
À partir de cette distribution, nous pouvons ensuite tracer au choix un pie plot (diagramme en secteurs) ou un barplot (diagramme en tuyaux d'orgues).
Si la variable est qualitative ordinale, il suffit de classer sur le graphique les modalités en ordre croissant.
Pour représenter une variable quantitative continue, l'histogramme est le plus adéquat. Il regroupe les différentes valeurs prises par la variable en classes.
Pour représenter une variable quantiative discrète, on privilégiera un diagramme en bâtons.
Nous pouvons aussi représenter une variable sous forme de tableau – voyons quand et comment dans le chapitre suivant !
