Objectifs
Le meilleur moyen d'explorer des données complexes consiste à construire des représentations graphiques appropriées. Il est élémentaire et très utile de visualiser la nature de la liaison entre deux variables quantitatives avec un nuage de points ; c'est rappelé dans le tutoriel de statistique descriptive ( ).
Lorsque ce sont variables avec qui sont observées, il reste possible de construire une matrice de nuages de points croisant toutes les variables 2 à 2 si n'est pas trop grand mais l'analyse en composantes principales (ACP) apporte une solution plus satisfaisante surtout avec grand.
Considérons variables quantitatives observées sur individus ou unités statistiques. L'objectif de l'ACP est de construire une double représentation graphique :
représentation plane, ou de petite dimension, du nuage de points des individus en respectant au mieux leurs positions respectives, leurs distances deux à deux ;
représentation des variables illustrant la structure des corrélations linéaires entre celles-ci.
D'un point de vue statistique, l'ACP est la recherche de nouvelles variables, combinaisons linéaires des variables initiales et orthogonales deux à deux, de sorte que la variance de la première combinaison soit la plus grande puis celle de la deuxième, orthogonale à la précédente, soit à nouveau de plus grande variance, etc.
Il est aussi possible de proposer une analogie physique. Considérons l'ensemble des points ou individus dans l'espace . Ils constituent un solide dont les axes d'inertie sont déterminés par les vecteurs propres de la matrice d'inertie de ce solide. Ces vecteurs propres définissent les axes de plus grande dispersion des points du nuage ou solide.
Exemple jouet
Les données
Une présentation très élémentaire de cette démarche est proposée sur un exemple jouet de données. Considérons les notes (de 0 à 20) obtenues par 9 élèves dans 4 disciplines (mathématiques, physique, français, anglais) :
| MATH | PHYS | FRAN | ANGL |
Jean | 6.00 | 6.00 | 5.00 | 5.50 |
Alan | 8.00 | 8.00 | 8.00 | 8.00 |
Anni | 6.00 | 7.00 | 11.00 | 9.50 |
Moni | 14.50 | 14.50 | 15.50 | 15.00 |
Didi | 14.00 | 14.00 | 12.00 | 12.50 |
Andr | 11.00 | 10.00 | 5.50 | 7.00 |
Pier | 5.50 | 7.00 | 14.00 | 11.50 |
Brig | 13.00 | 12.50 | 8.50 | 9.50 |
Evel | 9.00 | 9.50 | 12.50 | 12.00 |
Il est classique d'analyser séparément chacune de ces 4 variables, soit en faisant un graphique, soit en calculant des résumés numériques. Les liaisons entre 2 variables (par exemple mathématiques et français), sont illustrées en faisant un graphique du type nuage de points et évaluées en calculant leur coefficient de corrélation linéaire.
Mais comment faire une étude simultanée des 4 variables, ne serait-ce qu'en réalisant un graphique ?
La difficulté vient de ce que les individus (les élèves) ne sont plus représentés dans un plan, espace de dimension 2, mais dans un espace de dimension 4, chacun étant caractérisé par les 4 notes qu'il a obtenues.
L'objectif de l'analyse en composantes principales est de projeter les points sur un espace de dimension réduite (par exemple, ici, 2) en déformant le moins possible la réalité, c'est-à-dire les positions respectives des élèves entre eux. Il s'agit donc d'obtenir le résumé le plus pertinent des données initiales.
Descriptions uni- et bivariée
Tout logiciel statistique fournit la moyenne, l'écart-type, le minimum et le maximum de chaque variable. Il s'agit donc, pour l'instant, d'études univariées.
Statistiques élémentaires
Variable | Moyenne | Écart-type | Minimum | Maximum |
MATH | 9.67 | 3.37 | 5.50 | 14.50 |
PHYS | 9.83 | 2.99 | 6.00 | 14.50 |
FRAN | 10.22 | 3.47 | 5.00 | 15.50 |
ANGL | 10.06 | 2.81 | 5.50 | 15.00 |
Notons au passage la grande homogénéité des 4 variables considérées : même ordre de grandeur pour les moyennes, les écarts-types, les minima et les maxima.
Le tableau suivant est la matrice des corrélations. Elle donne les coefficients de corrélation linéaire des variables prises deux à deux. C'est une succession d'analyses bivariées, constituant un premier pas vers l'analyse multivariée.
Coefficients de corrélation
| MATH | PHYS | FRAN | ANGL |
MATH | 1.00 | 0.98 | 0.23 | 0.51 |
PHYS | 0.98 | 1.00 | 0.40 | 0.65 |
FRAN | 0.23 | 0.40 | 1.00 | 0.95 |
ANGL | 0.51 | 0.65 | 0.95 | 1.00 |
Remarquons que toutes les corrélations linéaires sont positives, ce qui signifie que toutes les variables varient, en moyenne, dans le même sens, certaines étant très fortes (0.98 et 0.95), d'autres moyennes (0.65 et 0.51), d'autres enfin plutôt faibles (0.40 et 0.23).
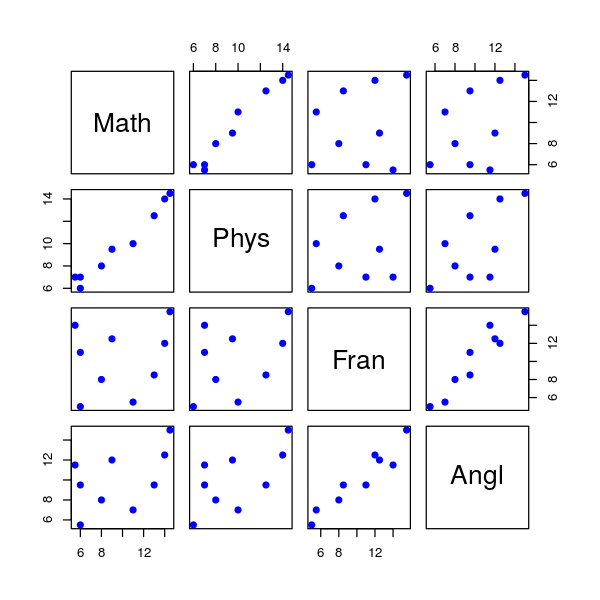
La figure ci-dessus fournit la matrice des nuages de points en considérant toutes les variables deux à deux. Le principal objectif de cette représentation est de s'assurer qu'il n'existe pas de liaison non linéaire entre les variables. En effet, une telle liaison serait négligée par des indicateurs (corrélation) ou toute analyse linéaire comme l'ACP ou la régression.
Décomposition spectrale de la matrice des covariances
Résultats numériques
Continuons l'analyse par l'étude de la matrice des variances-covariances. La diagonale de cette matrice fournit les variances des 4 variables considérées.
Matrice des variances-covariances :
| MATH | PHYS | FRAN | ANGL |
MATH | 11.39 | 9.92 | 2.66 | 4.82 |
PHYS | 9.92 | 8.94 | 4.12 | 5.48 |
FRAN | 2.66 | 4.12 | 12.06 | 9.29 |
ANGL | 4.82 | 5.48 | 9.29 | 7.91 |
Le tableau ci-dessous fournit les valeurs propres de la matrice des variances-covariances. Notez que la somme des valeurs propres est aussi la somme des variances ou trace de la matrice des covariances. D'un point de vue théorique, la trace d'un endomorphisme ne dépend pas de la base de représentation. Elle est identique dans la base canonique : matrice des covariances, ou celle des vecteurs propres : matrice diagonale des valeurs propres.
Valeurs propres ; variances expliquées :
FACTEUR | VAL. PR. | PCT. VAR. | PCT. CUM. |
1 | 28.23 | 0.70 | 0.70 |
2 | 12.03 | 0.30 | 1.00 |
3 | 0.03 | 0.00 | 1.00 |
4 | 0.01 | 0.00 | 1.00 |
| 40.30 | 1.00 |
|
Interprétation statistique
Chaque ligne du tableau ci-dessus correspond à une variable virtuelle (facteur ou variable principale) dont la colonne VAL. PR. (valeur propre) fournit la variance. Un facteur ou variable principale est une combinaison linéaire des variables initiales, dans laquelle les coefficients sont donnés par les coordonnées des vecteurs propres (changement de base).
Rappelons que l'ACP peut être définie comme la recherche des combinaisons linéaires de plus grande variance des variables initiales (les valeurs propres).
La colonne PCT. VAR., ou pourcentage de variance, correspond au pourcentage de variance de chaque ligne par rapport au total. La colonne PCT. CUM. représente le cumul de ces pourcentages en dimension 1, 2... Additionnons maintenant les variances des 4 variables initiales (diagonale de la matrice des variances-covariances) :
La dispersion totale des individus considérés, en dimension 4, est ainsi égale à 40.30.
Additionnons par ailleurs les 4 valeurs propres obtenues :
Le nuage de points en dimension 4 est toujours le même et sa dispersion globale n'a pas changé.
Il s'agit d'un simple changement de base dans un espace vectoriel.
Par conséquent, les graphiques en dimension 2 présentés ci-dessous résument presque parfaitement la configuration réelle des données qui se trouvent en dimension 4. L'objectif de résumé pertinent des données en plus petite dimension est donc atteint.
Interprétation géométrique
Une autre interprétation est d'ordre géométrique. Chaque individu (resp. variable ) est considéré comme un vecteur à p (resp. ) composantes dans un espace vectoriel. L'ACP est la recherche du meilleur plan (ou sous-espace affine) de projection : le plus proche au sens des moindres carrés, pour obtenir la représentation la plus fidèle, ou la moins déformée, des individus (resp. des variables) dans un sous-espace de dimension réduite.
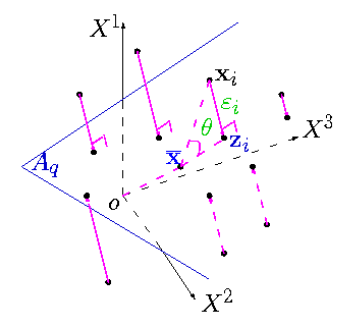
Sur ce graphique, est la projection orthogonale de , définie par le vecteurs des valeurs , sur le plan qui passe par le barycentre du nuage des points.
ACP réduite ou non
Les sections précédentes mettent l'accent sur la matrice de variance et sa décomposition en éléments propres. Les variables de ces données fictives présentent de bonnes propriétés, elles sont de même unité, toutes des notes, et de variances homogènes.
Dans le cas contraire, hétérogénéité des unités ou des variances, il est important d'apporter une forme de normalisation. En effet, comme la variance dépend de l'unité choisie ou même si une ou des variables ont de très grandes variances par rapport aux autres variables, cela peut avoir un effet délétère sur l'intérêt de l'ACP. Une seule variable, celle évidemment de grande variance, peut à elle seule accaparer le premier axe au détriment de la compréhension globale des relations entre les variables.
C'est la raison pour laquelle, si les variables ne partagent pas la même unité ou si de toute façon les variances sont hétérogènes, il est vivement conseillé de réduire (standardiser) les variables en les divisant par leur écart-type. Toutes les variables sont alors sans unité et de variance 1, elles jouent le même rôle et leur structure de corrélation est mise en exergue.
Étude des variables
Résultats numériques
Un résultat important pour aider à l'interprétation est fourni par le tableau des corrélations variables-facteurs. Il s'agit des coefficients de corrélation linéaire entre les variables initiales et les nouvelles variables dites principales ou facteurs.
Ce sont ces corrélations qui vont permettre de donner une signification aux facteurs ou variables principales pour les interpréter.
Corrélations variables-facteurs :
| F1 | F2 | F3 | F4 |
MATH | 0.81 | -0.58 | 0.01 | -0.02 |
PHYS | 0.90 | -0.43 | -0.03 | 0.02 |
FRAN | 0.75 | 0.66 | -0.02 | -0.01 |
ANGL | 0.91 | 0.40 | 0.05 | 0.01 |
Les deux premières colonnes de ce tableau permettent, tout d'abord, de réaliser le graphique des variables ci-dessous.
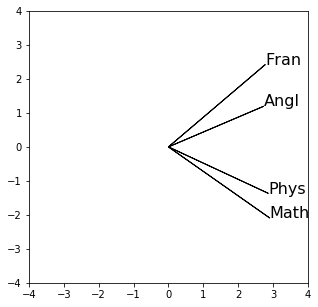
Noter que les deux dernières colonnes ne seront pas utilisées, puisque seulement deux dimensions sont nécessaires pour représenter les données.
Interprétation
Par construction, le cosinus de l'angle de deux vecteurs variables approche le coefficient de corrélation entre ces variables. Ainsi, on lit sur le graphique ci-dessus que le premier facteur est corrélé positivement, et assez fortement, avec chacune des 4 variables initiales : plus un élève obtient de bonnes notes dans chacune des 4 disciplines, plus il a un score élevé sur l'axe 1 ; réciproquement, plus ses notes sont mauvaises, plus son score est négatif.
Le premier facteur, combinaison des notes avec approximativement les mêmes coefficients positifs, représente la note moyenne (centrée sur la moyenne de la classe) de chaque élève.
En ce qui concerne l'axe 2, il oppose d'une part le français et l'anglais (corrélations positives) et, d'autre part, les mathématiques et la physique (corrélations négatives).
Le deuxième facteur est approximativement la moyenne des notes littéraires déduite de la moyenne des notes scientifiques.
Cette interprétation aide à comprendre la représentation des individus.
Étude des individus
Résultats numériques
Le tableau ci-dessous contient tous les résultats importants sur les individus.
Coordonnées des individus et cosinus carrés
| POIDS | PC1 | PC2 | COSCA1 | COSCA2 |
jean | 0.11 | -8.61 | 1.41 | 0.97 | 0.03 |
alan | 0.11 | -3.88 | 0.50 | 0.98 | 0.02 |
anni | 0.11 | -3.21 | -3.47 | 0.46 | 0.54 |
moni | 0.11 | 9.85 | -0.60 | 1.00 | 0.00 |
didi | 0.11 | 6.41 | 2.05 | 0.91 | 0.09 |
andr | 0.11 | -3.03 | 4.92 | 0.28 | 0.72 |
pier | 0.11 | -1.03 | -6.38 | 0.03 | 0.97 |
brig | 0.11 | 1.95 | 4.20 | 0.18 | 0.82 |
evel | 0.11 | 1.55 | -2.63 | 0.25 | 0.73 |
On notera que chaque individu représente 1 élément sur 9, d'où un poids (une pondération) de , ce qui est fourni par la première colonne du tableau ci-dessus.
Les 2 colonnes suivantes fournissent les coordonnées des individus (les élèves) sur les deux premiers axes (les facteurs) et ont donc permis de réaliser le graphique des individus ci-dessous. Elles sont appelées composantes principales ou valeurs prises par les individus sur les variables principales, combinaisons linéaires des variables initiales.

Interprétation
L'axe 1 représente le résultat d'ensemble des élèves : leur score – ou coordonnée – sur l'axe 1 fournit le même classement que leur moyenne générale. Par ailleurs, l'élève "le plus haut" sur le graphique, celui qui a la coordonnée la plus élevée sur l'axe 2, est Pierre dont les résultats sont les plus contrastés en faveur des disciplines littéraires (14 et 11.5 contre 7 et 5.5).
C'est exactement le contraire pour André qui obtient la moyenne dans les disciplines scientifiques (11 et 10) mais des résultats très faibles dans les disciplines littéraires (7 et 5.5). Monique et Alain ont un score voisin de 0 sur l'axe 2 car ils ont des résultats très homogènes dans les 4 disciplines, mais à des niveaux très distincts, ce qu'a déjà révélé l'axe 1.
Compléments à l'interprétation
Les 2 dernières colonnes du tableau sont des cosinus carrés qui fournissent la qualité de la représentation de chaque individu sur chaque axe. Ces quantités s'additionnent axe par axe, de sorte que, en dimension 2, Évelyne est représentée à 98 % (0.25 + 0.73), tandis que les 8 autres individus le sont à 100 %.
Avec les données initiales, chaque individu (chaque élève) est représenté par un vecteur dans un espace de dimension 4 (les éléments – ou coordonnées – de ce vecteur sont les notes obtenues dans les 4 disciplines). Résumé en dimension 2, et donc représenté dans un plan, chaque individu est alors représenté par la projection du vecteur initial sur le plan. Le cosinus carré relativement aux deux premières dimensions (par exemple, pour Évelyne, 0.98 ou 98 %) est celui de l'angle formé par le vecteur initial et sa projection dans le plan.
Plus le vecteur initial est proche du plan, plus l'angle en question est petit et plus le cosinus, et son carré, sont proches de 1 (ou de 100 %) : la représentation est alors très bonne. Au contraire, plus le vecteur initial est loin du plan, plus l'angle en question est grand (proche de 90 degrés) et plus le cosinus, et son carré, sont proches de 0 : la représentation est alors très mauvaise.
Représentation simultanée
Un troisième type de représentation graphique associant individus et variables (biplot) est détaillé dans le document décrivant plus précisément l'analyse en composantes principales. Ce graphe, représentant des vecteurs individus et variables appartenant à des espaces vectoriels différents, nécessite un développement plus détaillé pour en justifier la construction et l'interprétation.
Ce développement est basé sur la décomposition en valeurs singulières de la matrice des variables centrées. Géométriquement, le produit scalaire entre un vecteur variable et un vecteur individu fournit une approximation de la valeur de cette variable sur l'individu. Cela permet de comparer schématiquement la valeur prise par une variable sur un individu par rapport à la moyenne, le barycentre. Ainsi, Brigitte à une moyenne en maths supérieure à la moyenne de la classe mais inférieure à la moyenne de la classe en français. Monique a des notes plus grandes que la moyenne de la classe dans toutes les matières.
Cette représentation n'est possible que pour des jeux de données restreints : lorsque les dimensions sont trop importantes, elle devient illisible. Elle a été produite par la commande de R plutôt qu'avec Python comme pour les autres graphiques. Notons que les signes des axes ont changé avec le changement de logiciel. Plus précisément, le signe d'un vecteur propre n'est pas une information pertinente et peut changer d'un logiciel à l'autre. Ce qui est important, c'est la direction portée par le vecteur propre et pas sa direction. L'interprétation est d'ailleurs identique.
L'analyse factorielle discriminante, cas particuler d'ACP
Considérons la même situation que celle de l'ACP : variables quantitatives observées sur individus ou unités statistiques. Ajoutons l'observation d'une variable qualitative à classes pour définir l'analyse factorielle discriminante (AFD). Comme en ACP, l'objectif est de fournir une meilleure représentation graphique en petite dimension mais en tenant compte de l'observation de la variable qualitative, donc des classes.
L'objectif devient alors la recherche de la représentation privilégiant le plus possible les différences entre les classes d'individus au détriment des différences au sein des classes.
Principes de l'AFD
Comme vu précédemment, l'ACP est basée sur la recherche de combinaisons linéaires de plus grande variance. L'AFD se focalise sur la variance interclasses, pour mettre en évidence les différences des classes tout en cherchant à minimiser les effets de la variance intraclasse qui disperse les individus au sein de chaque classe.
La justification de l'AFD est détaillée dans une vignette de Wikistat. Il y est montré que l'AFD est un cas particulier optimal d'ACP permettant d'atteindre l'objectif de meilleure représentation des classes. L'AFD est finalement l'ACP des barycentres des classes afin de mettre en exergue la variance interclasses, mais en affectant l'espace des individus d'une métrique particulière, dite de Mahalanobis. Pour minimiser l'effet de la variance intraclasse considérée comme parasite, du bruit, la métrique de Mahalanobis est définie par la matrice inverse de la variance intraclasse, matrice carrée symétrique définie positive.
Deux techniques cohabitent sous la même appellation d'analyse discriminante ; celle :
descriptive ou exploratoire qui vise la meilleure représentation graphique des classes ;
décisionnelle qui, connaissant pour un individu donné les valeurs des , cherche à prédire la classe inconnue de la variable qualitative.
Il faut lire l'AFD comme un préalable à la construction d'une analyse discriminante décisionnelle ou à tout autre méthode ou algorithme de classification supervisée. L'objectif principal est de représenter les qualités discriminatoires des variables quantitatives pour séparer correctement les classes de la variable qualitative. Le graphique des individus permet d'apprécier la qualité de discrimination tandis que, si le nombre de variables n'est pas trop grand, une représentation des variables permet, comme en ACP, d'expliquer la discrimination des classes par les variables quantitatives.
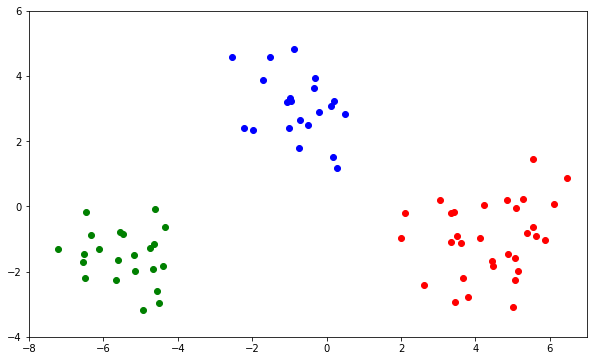
Exemple jouet : les insectes de Lubitsch
Cette méthode est illustrée par une comparaison des sorties graphiques issues d'une ACP et d'une AFD. Les données décrivent trois classes d'insectes sur lesquels ont été réalisées 6 mesures anatomiques sur les ailes, élytres, antennes, pattes des insectes. On cherche à savoir si ces mesures permettent de retrouver la typologie de ces insectes. Ce jeu de données académique conduit à une discrimination assez évidente. La comparaison entre l'ACP et l'AFD met clairement en évidence le rôle de la distance de Mahalanobis sur la forme des nuages de chaque classe en analyse discriminante.
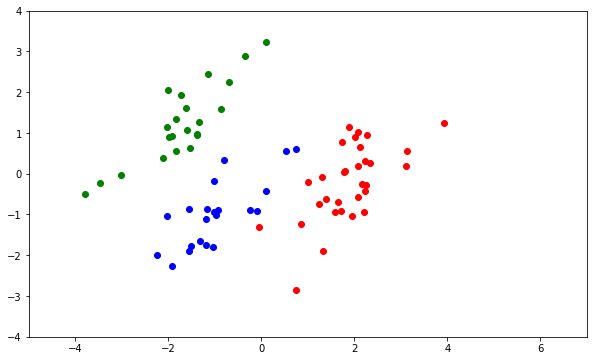
Les données académiques sont faciles à étudier, l'ACP ci-dessus montre déjà que les trois nuages d'insectes se distinguent assez bien dans le premier plan principal. Observons la forme identique des trois nuages ; les trois classes partagent approximativement la même matrice de variance qui est aussi la variance intraclasse.
Le graphique ci-dessous représente les variables et plus précisément leur structure de corrélation.
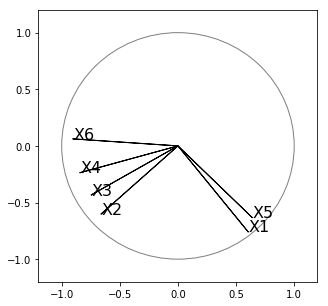
Le cercle présent sur le graphique est appelé cercle des corrélations. Il est défini par l'intersection de la boule unité avec le plan de projection des vecteurs variables. Les variables sont centrées et surtout réduites, divisées par leur écart type. Dans ce cas, ce sont des vecteurs de longueur 1 donc placés sur la boule unité. Ils se projettent nécessairement tous à l'intérieur du cercle. Le cercle des corrélations est une aide graphique pour apprécier la qualité de représentation de chaque variable. Plus une variable est proche du cercle, meilleure est sa représentation.
Dans le cas contraire, le vecteur variable présente un angle grand, proche de 90°, avec le plan de projection, et sa représentation est mauvaise ; ne pas en tenir compte dans l'interprétation.
L'AFD produit le graphique ci-dessous. Cette ACP des barycentres des classes sépare encore mieux les classes d'insectes et surtout, le changement de métrique rend sphérique la forme des classes qui sont donc mieux regroupées autour de leur barycentre.