Après avoir vu, dans les chapitres précédents, les notions de données, de coût et de modèle nous allons aborder la notion de généralisation, fondamentale pour maitriser les enjeux de l'apprentissage automatique. Nous allons donc :
voir comment mesurer la qualité d'un modèle,
motiver l'importance de la généralisation à travers un exemple,
définir la généralisation et son lien avec la complexité des modèles,
en tirer des conséquences pour le processus d'apprentissage lui-même, en introduisant les mécanismes de contrôle de la complexité.
Trois types de données utilisées en apprentissage
Apprentissage et généralisation
Nous avons vu, dans la leçon précédente, qu'un modèle qui a bien appris se doit de donner de bons résultats sur de nouvelles données.
De quoi parle-t-on quand on parle d'erreur en apprentissage statistique ?
On distingue alors deux types d'erreurs :
l'erreur d'apprentissage, calculée sur les données ayant été utilisée pour apprendre un modèle,
l'erreur de généralisation, qui est la mesure de performance du modèle en production, calculée sur des données futures.
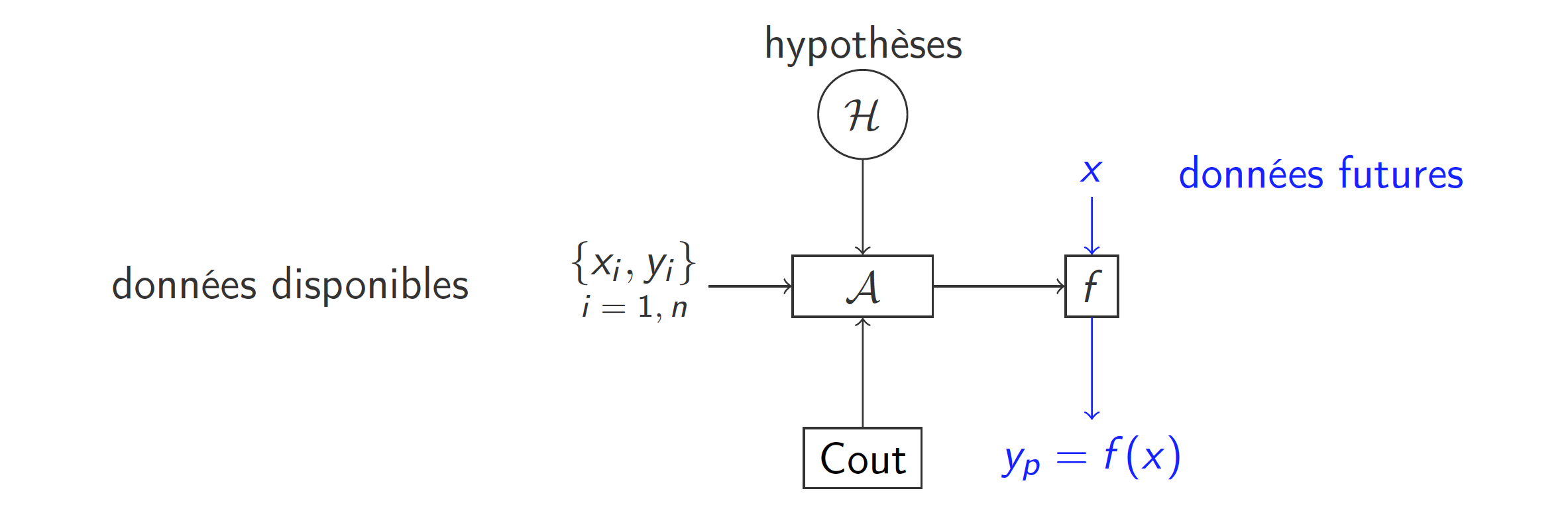
Pour que cette évaluation soit pertinente, il est indispensable que les données utilisées pour l’évaluation soient différentes des données ayant été utilisées pour l'apprentissage, car en apprentissage aussi on ne peut pas être à la fois juge et partie.
Apprentissage et complexité des modèles
Nous avons vu qu'en apprentissage, à cause de la propriété d'universalité, il existait de nombreux modèles possibles permettant d'apprendre et d'ajuster la complexité du modèle à celle du problème sous-jacent aux données. Il est nécessaire, pour bien apprendre, de savoir comparer les modèles et donc d'être en mesure de les évaluer. Une manière de réaliser cette évaluation consiste à utiliser des données pour comparer, sur des cas réels, les performances d'un modèle.
Il est donc recommandé, quand on a suffisamment de données, de répartir les données disponibles en trois groupes :
les données utilisées pour ajuster les paramètres du modèle : ce sont les plus nombreuses et elles constituent l'ensemble d'apprentissage ;
les données utilisées pour comparer les modèles : elles forment l'ensemble de validation ;
les données permettant d'évaluer les performance d'un modèle d'apprentissage : c'est l'ensemble de test.
Typiquement, lorsqu'on dispose de beaucoup de données, il est d'usage d'en prendre 60 à 70 % pour l'apprentissage et d'en garder 15 à 20 % pour la validation et le test.

Quand on ne dispose pas de beaucoup de données, il ne faut pas procéder de cette manière. Il faut utiliser d'autres approches pour évaluer les modèles (comme le ré-échantillonnage) ou avoir recours à la théorie.
L'apprentissage poursuit deux objectifs qui peuvent s'avérer contradictoires. Il faut trouver un modèle qui minimise le coût sur les données disponibles et qui généralise bien. La contradiction entre les deux objectifs est liée au fait que, pour minimiser le coût sur l'ensemble d'apprentissage, il faut augmenter la capacité du modèle, ce qui peut entraîner l'apprentissage du bruit et donc une diminution de sa généralisation.
C'est la recherche du compromis entre erreur d'apprentissage et capacité du modèle que l'on appelle le contrôle de la complexité.
Généralisation et complexité
Un exemple illustratif
Nous allons illustrer les enjeux du contrôle de la complexité sur un exemple jouet.
Définir les courbes d'apprentissage et de validation (ou de test)
Afin de caractériser ces phénomènes de sous et sur apprentissage, on peut représenter l'évolution des erreurs d'apprentissage et de test en fonction de la complexité du modèle. Pour ce faire, on considère une famille d'ensembles gigognes inclus les uns dans les autres (comme par exemple l'ensemble des polynômes de degré avec différents ).
Pour chacune de ces classes de modèles (pour chaque k dans notre exemple), on apprend sur des données d'apprentissage et l'on évalue la qualité du modèle sur des données de test ou de validation.
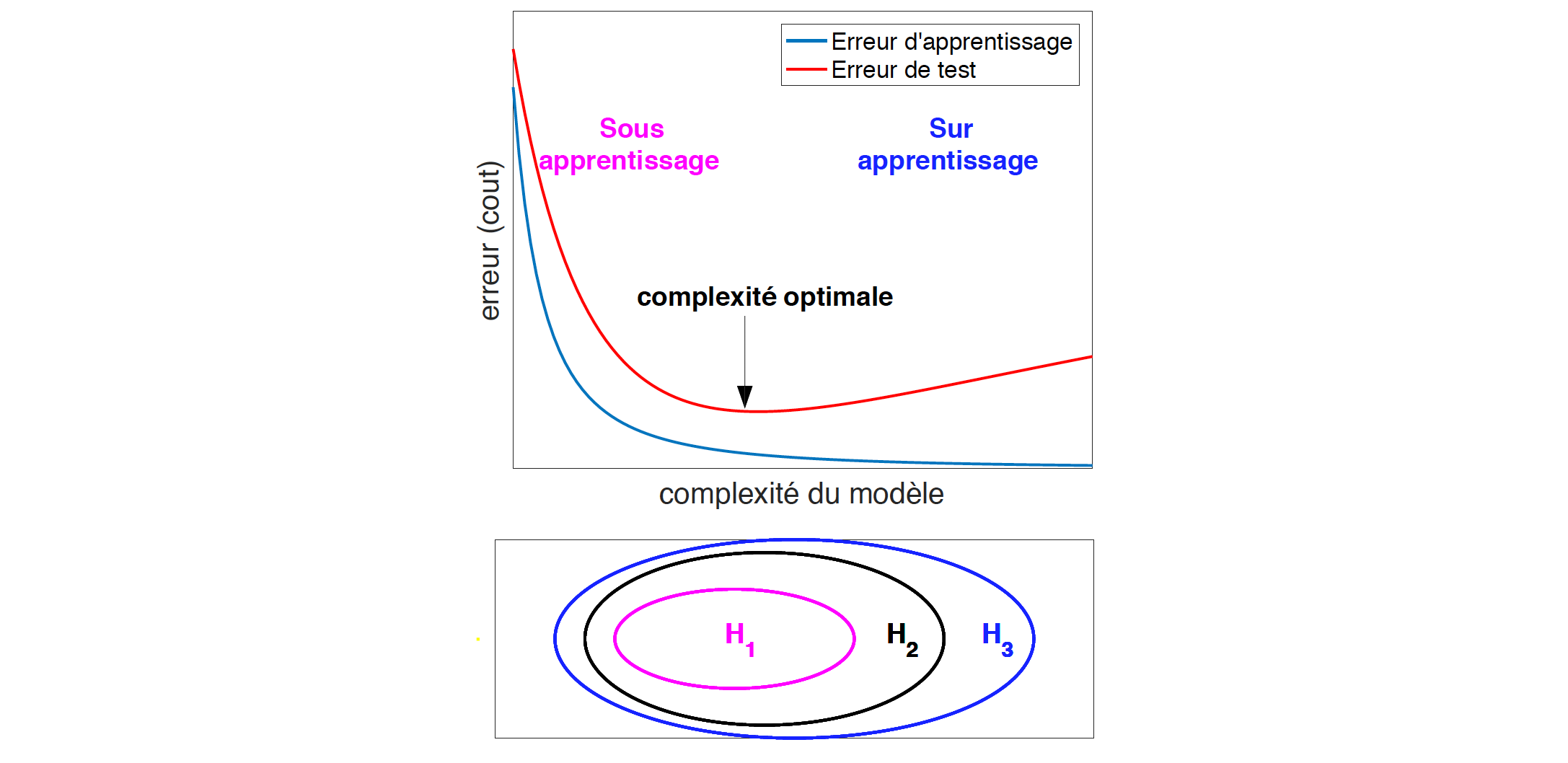
Plus la complexité augmente, plus le modèle a la capacité d’assimiler les données et plus l'erreur d'apprentissage diminue. L'erreur de validation en fonction de la complexité a une forme en « u ». Lorsque la complexité des modèles augmente, elle commence par descendre en régime de sous-apprentissage et remonte quand le régime de sur-apprentissage est atteint.
Le compromis biais/variance est une autre manière de décrire ce problème de contrôle de la complexité. Si le modèle n'est pas assez complexe, il n'est pas possible de modéliser correctement la fonction à apprendre. On parle de biais d'induction. Si le modèle est trop grand, l'apprentissage devient trop sensible au bruit contenu dans les données et c'est un terme de variance qui devient dominant.
Comment mesurer la complexité d’un modèle ?
Qu'est-ce que la complexité d'un modèle ?
Le contrôle de la complexité en apprentissage statistique a plusieurs dimensions. Il peut être associé au modèle lui-même, à la manière dont on utilise les données ou encore à la méthode d'optimisation employée. On parle parfois d'effet régularisant pour décrire ces mécanismes permettant d'obtenir des ensembles gigognes de modèles.
La complexité du modèle lui même
La complexité du modèle, s'il est dénombrable, peut être définie par son cardinal. Elle peut aussi être définie par sa taille (son nombre de paramètres). Elle peut être implicitement contrôlée par une mesure de régularité comme une norme. On considère alors l'ensemble des modèles dont la norme est inférieure à une quantité positive, que l'on ajuste selon la complexité désirée. Il est aussi possible de la contrôler implicitement à travers une pénalité ou un terme de régularisation (là encore comme une norme par exemple).
La régularisation par les données
La taille des données, notamment le nombre de variables explicatives, permet de jouer sur la complexité des modèles. Il est aussi possible de régulariser un modèle grâce à l'injection de bruit. L'idée est d'augmenter artificiellement l'ensemble d'apprentissage, en considérant de nouvelles données d'apprentissage obtenues par l'ajout de bruit à des exemples connus. Plus la variance du bruit ajouté est importante, plus le modèle appris est régulier.
La régularisation liée à l’optimisation
L'algorithme d'apprentissage lui-même peut avoir des effets régularisants. C'est le cas par exemple de l'arrêt prématuré de l'apprentissage (early stopping). En effet, lors de l'apprentissage de modèles universels, on peut observer un phénomène de semi convergence de l'erreur de généralisation, qui commence par décroître puis qui augmente après un certain temps d'apprentissage. L'utilisation de certaines méthodes comme le gradient stochastique a aussi des effets régularisants.
Complexité et apprentissage
Il est important de noter que toutes ces méthodes de régularisation introduisent un biais associé à une hypothèse a priori sur la nature de la solution. Ainsi, il n'est pas possible de trouver une méthode meilleure que les autres dans tous les cas. Ce résultat négatif est associé au théorème « pas de repas gratuit » (no free lunch theorem).
D'un point de vue pratique, il est donc recommandé d'utiliser plusieurs techniques de régularisation. Souvent, les algorithmes d'apprentissage combinent la sélection de variable, un terme de pénalité, de l'injection de bruit et un gradient stochastique avec arrêt prématuré.
L'apprentissage comme un problème d'optimisation bi-objectif
L'apprentissage statistique peut être vu comme un problème d'optimisation bi-objectif. Il s'agit de minimiser simultanément l’erreur d’apprentissage et la complexité du modèle. Il est parfois associé au principe du rasoir d'Occam.
En résumé
Bien apprendre, c’est avoir la faculté de généraliser et non apprendre par cœur. Pour mesurer la capacité de généralisation d'un modèle, il faut disposer d’un ensemble de test (voire de validation) et donc tout apprentissage doit commencer par une répartition des données disponibles en trois ensembles d'apprentissage, de validation de de test.
Bien généraliser requiert l'usage de mécanismes de régularisation pour contrôler la complexité du modèle. Comme aucun n'est systématiquement supérieur aux autres, il est préférable, en pratique, d'en utiliser plusieurs simultanément. Du coup, l'apprentissage peut être associé à un problème d'optimisation bi-critère ou l'on cherche à minimiser l’erreur d’apprentissage et la complexité du modèle.
Nous allons maintenant détailler les méthodes de base de l'apprentissage statistique.
