• 12 hours
  • Medium
License

Free online content available in this course.

course.header.alt.is_video

course.header.alt.is_certifying

Got it!

Last updated on 1/29/24

Réalisez les machines à vaste marge (SVM) pour la classification

L'objectif du cours est de :

  • comprendre les séparateurs à vaste marge (support vector machine),

  • mettre en œuvre cette méthode pour la classification binaire et multi-classe,

  • maîtriser l'utilisation de l'astuce du noyau pour adapter les SVM à des problèmes non-linéaires.

Nous allons étudier les SVM (support vector machine ou séparateur à vaste marge) pour la classification. Nativement, les SVM cherchent à estimer une fonction de score qui maximise  la séparation entre les classes, c'est-à-dire la marge. Les SVM se prêtent aussi à une généralisation du modèle de classification à des problèmes non-linéaires en utilisant le formalisme des noyaux. Pour rentrer dans le sujet, commençons par la notion de marge.

Comprenez la notion de marge

Démarrons par un problème de classification binaire, dont l'objectif est précisé ci-dessous.

Prenons un problème de classification comme sur la figure 1.

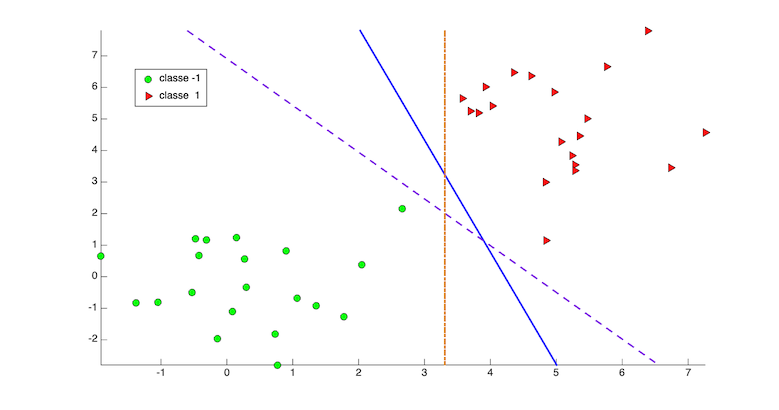
Classes linéairement séparables
Figure 1 : Classes linéairement séparables

On peut trouver plusieurs hyper-plans de séparation parfaite des classes. Laquelle choisir ? Il faut privilégier la solution qui maximise la marge entre les points des deux classes.

Comment définir la marge ?

Quelques notions de géométrie permettent de montrer que la distance du point $\(\mathbf{x}\)$ à l'hyper-plan $\(H\)$ d'équation $\(f(\mathbf{z}) = \beta_0 + \mathbf{z}^\top \boldsymbol{\beta} = 0\)$ (la frontière de séparation) est $\(\text{dist}(\mathbf{x}, H) = \frac{| \beta_0 + \mathbf{x}^\top \boldsymbol{\beta}|}{\|\boldsymbol{\beta}\|} \)$ . Si nous définissons notre fonction de classification telle que

$\[\left \{ \begin{array}{lll} \min_{\mathbf{x}_i} & \beta_0 + \mathbf{x}_i^\top \boldsymbol{\beta} = 1 & \forall i, \, y_i = 1 \\ \max_{\mathbf{x}_j} & \beta_0 + \mathbf{x}_j^\top \boldsymbol{\beta} = -1 & \forall j, \, y_j = -1 \end{array} \right.\hspace{100pt} (1)\]$

, alors la $\(\text{Marge} = \frac{2}{\|\boldsymbol{\beta}\|}\)$ . La figure 2 montre cette marge.

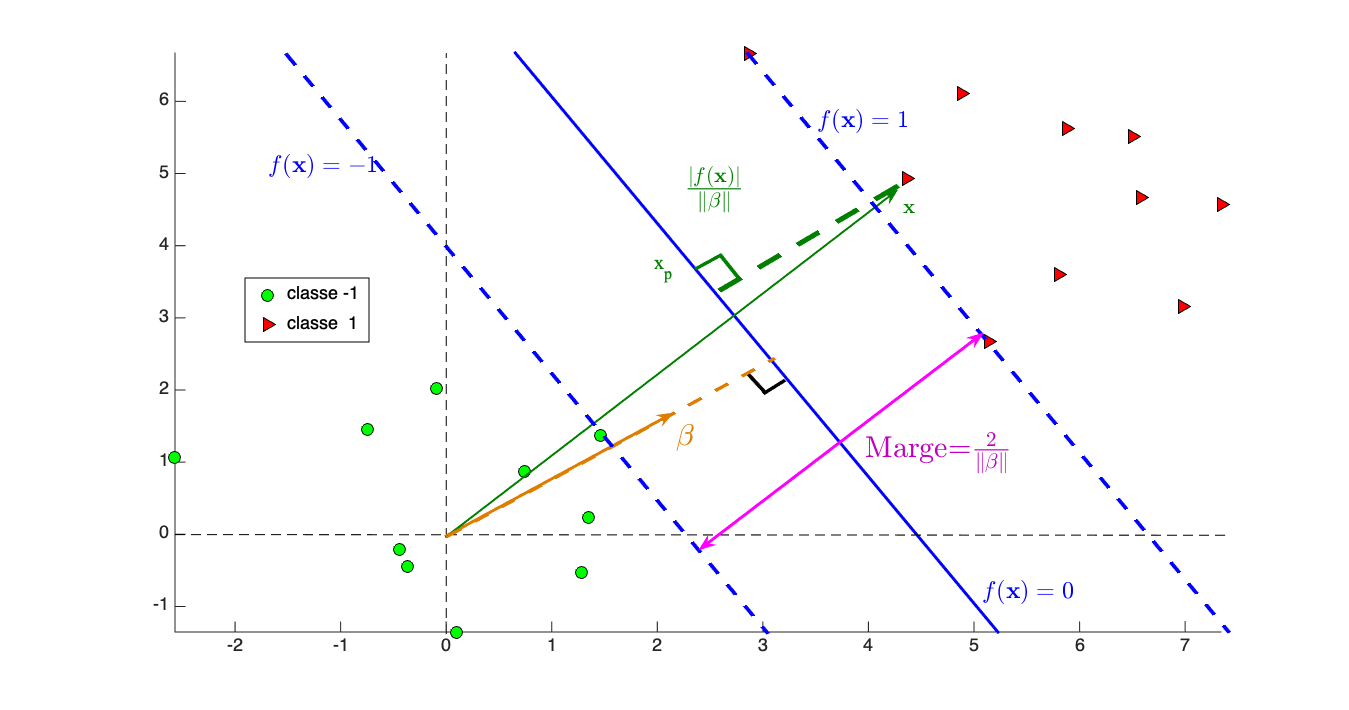
Illustration de la notion de marge. Les pointillés en bleu correspondent à la séparation définie en (1)
Figure 2 : Illustration de la notion de marge. Les lignes pointillées en bleu correspondent à la frontière de séparation définie en (1).

Maximisez la marge

Pour trouver notre fonction de classification, il faut :

  • maximiser la marge $\(\max_{\boldsymbol{\beta}} \frac{2}{\|\boldsymbol{\beta}\|} \,\, \Longleftrightarrow \min_{\boldsymbol{\beta}} \,\, \frac{\|\boldsymbol{\beta}\|^2}{2}\)$,

  • s'assurer que tous les points sont bien classés, c'est-à-dire $\(y_i(\beta_0 + \mathbf{x}_i^\top \boldsymbol{\beta}) \geq 1, \quad \forall \, i=1,\cdots, n\)$ compte tenu de la définition de l'équation (1).

Gérez les erreurs de classification

L'exemple de la figure 2 est un cas idéal. En pratique, tous les points ne peuvent pas être classés correctement. Il faut alors relâcher les contraintes $\(y_i(\beta_0 + \mathbf{x}_i^\top \boldsymbol{\beta}) \geq 1\)$ et autoriser $\(y_i(\beta_0 + \mathbf{x}_i^\top \boldsymbol{\beta}) \geq 1 - \xi_i\)$ avec le terme d'erreur $\(\xi_i \geq 0\)$ .

Ces termes d'erreurs (voir la figure 3) doivent être intégrés dans la formulation du problème SVM en trouvant un compromis entre la maximisation de la marge et le contrôle des erreurs.

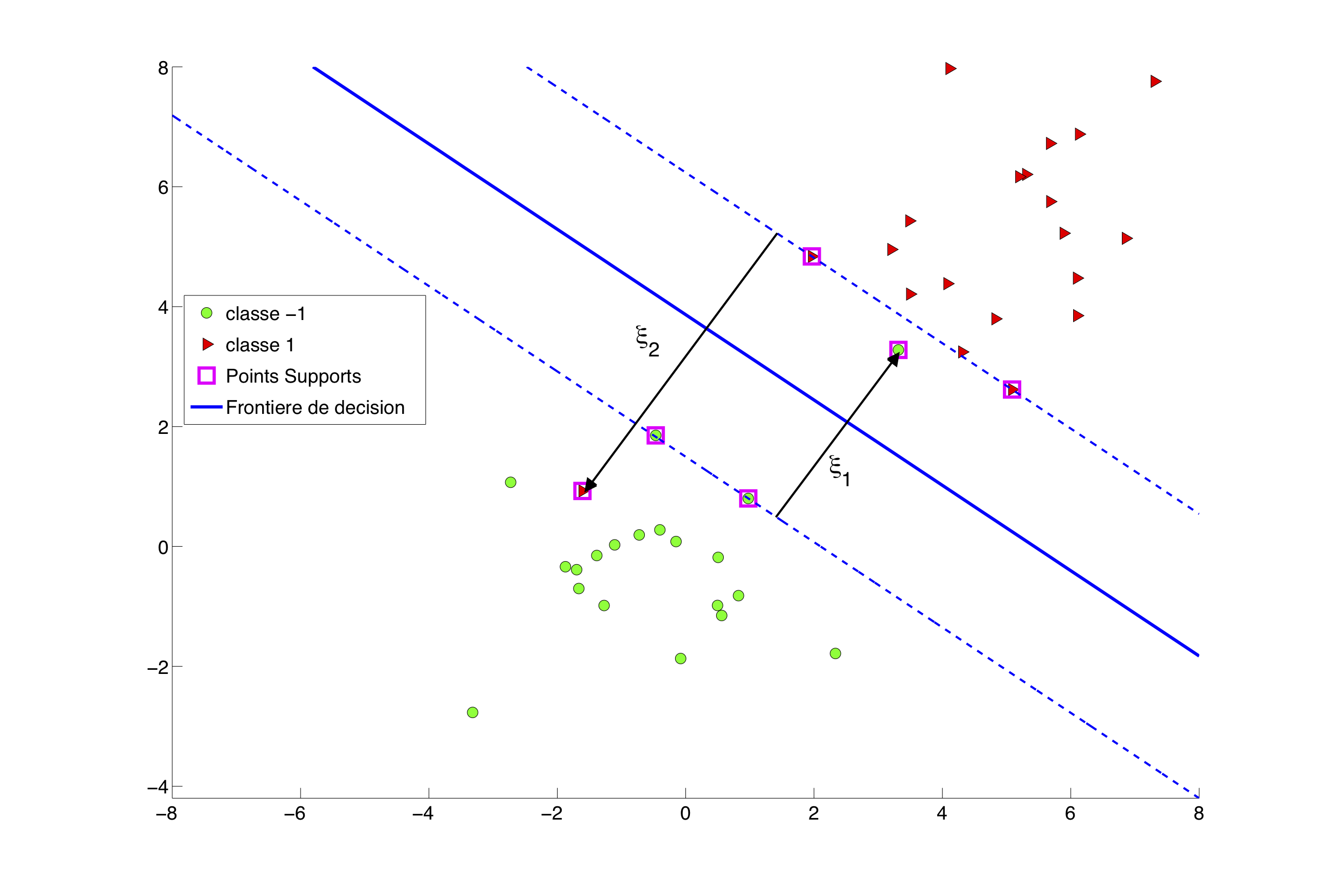
SVM linéaire autorisant des erreurs de classification
Figure 3 : SVM linéaire autorisant des erreurs de classification (points situés dans la marge ou du mauvais côté de la frontière de séparation)

Le choix de  $\(C\)$ influence la taille de la marge et les erreurs de classification comme sur les figures 4-a et 4-b.

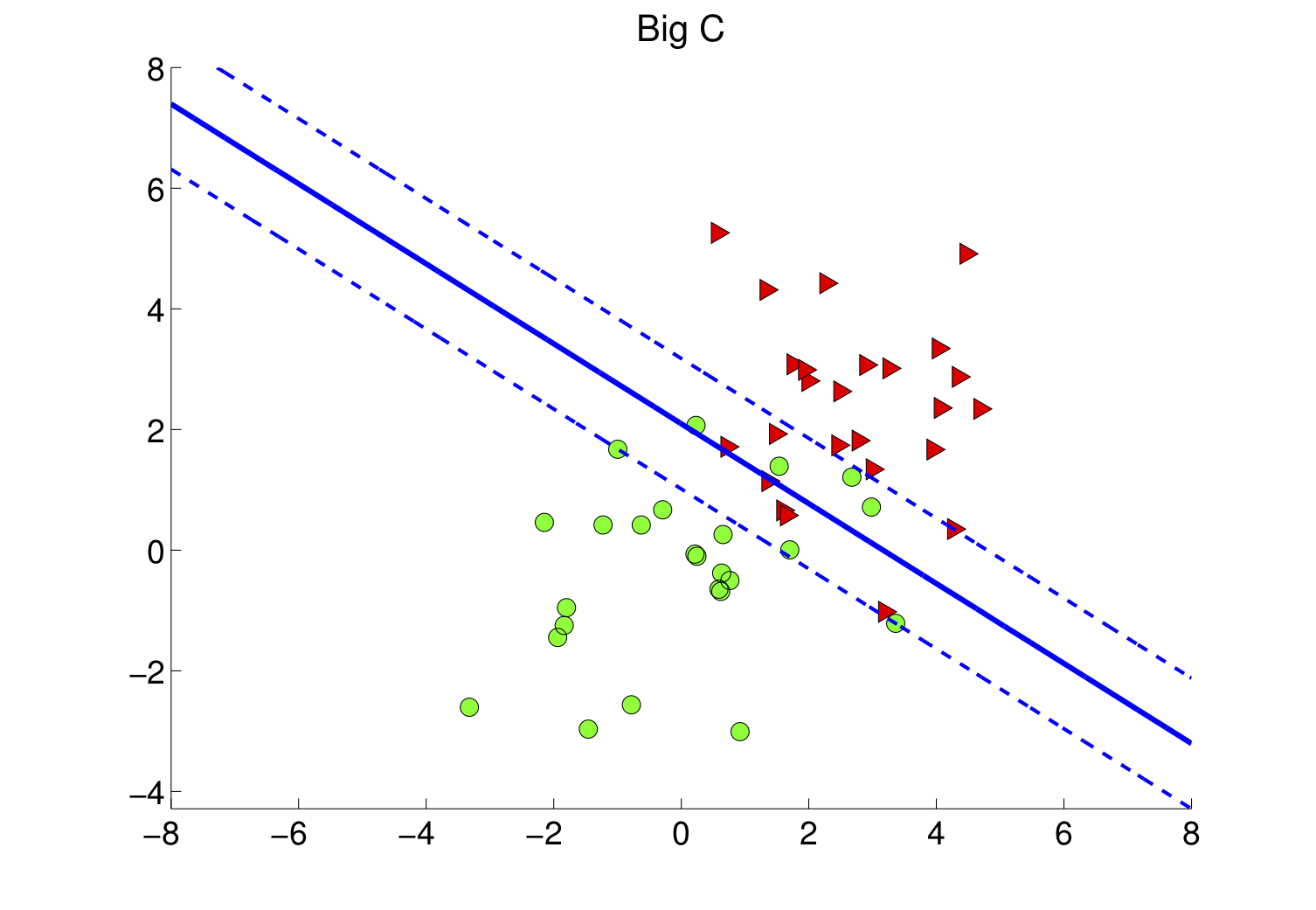
Figure 4-a : Une grande valeur de C conduit à une petite marge
Figure 4-a : Une grande valeur de C conduit à une petite marge.

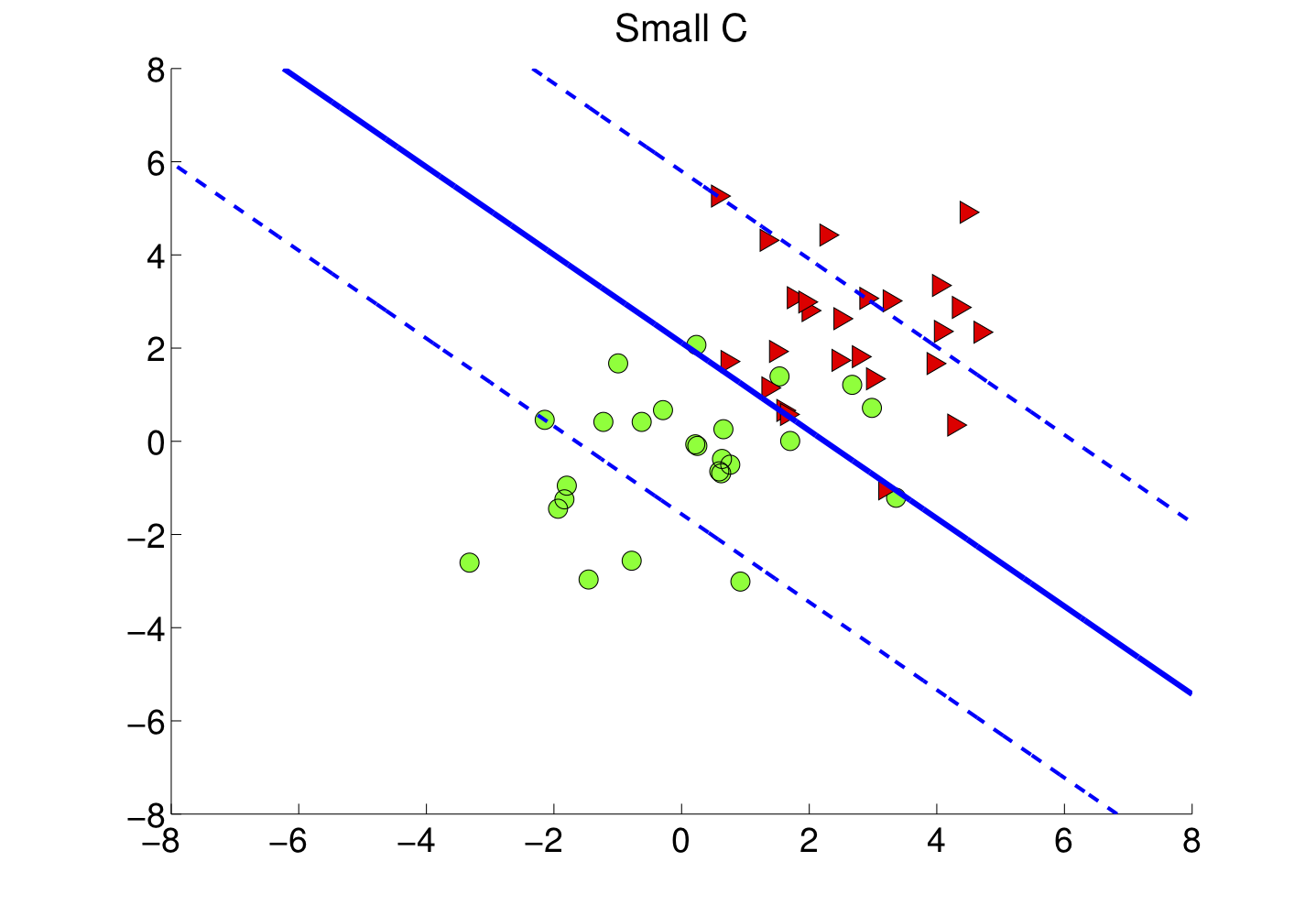
Figure 4-b : En diminuant C on agrandit la marge.
Figure 4-b : En diminuant C on agrandit la marge.

Comprenez la résolution du problème SVM

Le problème (2) est un problème d'optimisation avec $\((2n)\)$ contraintes inégalités. Pour le résoudre, l'idée est de se débarrasser des contraintes en le transformant en un problème sans contraintes. Pour cela, à chaque inégalité on associe un paramètre positif dit de Lagrange et on définit la fonction lagrangienne comme

$\[L(\beta_0, \boldsymbol{\beta}, \{\xi_i\}, \{\alpha_i\}, \{\eta_i\}) = \frac{1}{2}\|\boldsymbol{\beta} \|^2 + C \sum_{i=1}^n \xi_i - \sum_{i=1}^n \, \alpha_i \left[1 - \xi - y_i(\beta_0 + \boldsymbol{\beta}^\top \mathbf{x_i}) \right] - \sum_{i=1}^n \,\eta_i \xi_i\]$

avec $\(\alpha_i \geq 0\)$ et  $\(\eta_i \geq 0\)$,  $\(i=1, \cdots, n\)$ les paramètres de Lagrange (inconnus) associés respectivement aux inégalités (2a) et (2b). Le problème résultant consiste en

$\[\min_{\beta_0, \boldsymbol{\beta}, \{\xi_i\}} \max_{\{\alpha_i \geq 0\}, \{\eta_i \geq 0 \}} \,\,\, L(\beta_0, \boldsymbol{\beta}, \{\xi_i\}, \{\alpha_i \}, \{\eta_i \})\]$

c'est-à-dire à minimiser le pire cas où les contraintes ne seraient pas satisfaites,  les paramètres de Lagrange agissant comme des sortes de pénalités si ces contraintes ne sont pas respectées. Typiquement, $\(\alpha_i = 0\)$ si la contrainte (2a) correspondante est strictement vérifiée, c'est-à-dire $\(y_i(\beta_0 + \mathbf{x}_i^\top \boldsymbol{\beta}) > 1\)$ ; $\(\alpha_i\)$ est différent de 0 dans le cas contraire.

Comme notre problème initial (2) est convexe avec des contraintes affines, la théorie de l'optimisation nous dit que

$\[\min_{\beta_0, \boldsymbol{\beta}, \{\xi_i\}} \,\, \max_{\{\alpha_i \geq 0\}, \{\eta_i \geq 0 \}} \,\,\, L(\beta_0, \boldsymbol{\beta}, \{\xi_i\}, \{\alpha_i \}, \{\eta_i \}) = \max_{\{\alpha_i \geq 0\}, \{\eta_i \geq 0 \}} \,\, \min_{\beta_0, \boldsymbol{\beta}, \{\xi_i\}} \,\,\, L(\beta_0, \boldsymbol{\beta}, \{\xi_i\}, \{\alpha_i \}, \{\eta_i \})\]$

Du coup, les conditions d'optimalité du problème de minimisation de $\(L\)$ par rapport à $\(\boldsymbol{\beta}\)$ , $\({\beta}_0\)$ et $\(\xi_i\)$ donnent respectivement :

$\[\begin{eqnarray} \boldsymbol{\beta} - \sum_{i=1}^n y_i \, \alpha_i \,\mathbf{x}_i & = & 0 ,\, \Longrightarrow \,\, \boldsymbol{\beta} = \sum_{i=1}^n y_i \, \alpha_i \,\mathbf{x}_i \hspace{20pt} (3a) \\ \sum_{i=1}^n y_i \, \alpha_i & = & 0 \hspace{100pt} (3b) \\ C - \alpha_i - \eta_i & = & 0 \,\, \Longrightarrow \,\, \alpha_i \leq C \hspace{50pt} (3c) \end{eqnarray}\]$

Il nous suffit donc de connaitre les $\(\alpha_i \)$ pour obtenir $\(\boldsymbol{\beta}\)$ .

Si nous remplaçons les conditions d'optimalité dans $\(L\)$ et en utilisant la remarque ci-dessus, nous pouvons éliminer $\(\boldsymbol{\beta}\)$ , $\({\beta}_0\)$ et $\(\xi_i\)$ de $\(L\)$ dont l'expression dépendra uniquement des $\(\alpha_i \)$ . Ceci conduit au problème d'optimisation :

C'est quoi les points supports ?

Après résolution du problème dual, on peut montrer que les coefficients $\(\{\alpha_i\}_{i=1}^n\)$ peuvent être classés en trois groupes   :

  • Les points $\(\mathbf{x}_i\)$ qui sont bien classés et hors de la marge auront leur $\(\alpha_i = 0\)$ .

  • Les points $\(\mathbf{x}_i\)$ qui sont mal classés ou à l'intérieur de la marge sont caractérisés par $\(\alpha_i = C\)$ .

  • Les points se trouvant sur la marge auront $\(0 \leq \alpha_i \leq C\)$ .

Une conséquence directe est que dans l'expression (3a), le vecteur $\(\boldsymbol{\beta}\)$ n'est déterminé que par quelques points, ceux pour lesquels les coefficients $\(\alpha_i \)$ sont non nuls : ce sont les points supports de la solution (voir la figure 3).

Assemblons les pièces du puzzle

Pour apprendre un modèle SVM à partir de données d'apprentissage, il nous faut :

  • choisir le paramètre $\(C > 0\)$ ,

  • résoudre le problème dual pour avoir $\(\{\hat \alpha_i\}_{i=1}^n\)$ ; en déduire  $\(\hat{\boldsymbol{\beta}}\)$ par la formule (2a) et $\(\hat{\beta}_0\)$ .

Notre fonction de classification est

$\[\begin{eqnarray} f(\mathbf{x}) & = & \hat \beta_0 + \hat{\boldsymbol{\beta}}^\top \mathbf{x} \\ f(\mathbf{x}) & = & \hat \beta_0 + \sum_{i \in SV} \, \hat{\alpha}_i \, y_i \, \mathbf{x}_i^{\top} \mathbf{x} \hspace{120pt} (4) \end{eqnarray}\]$

où $\(SV\)$ représente l'ensemble des points supports.

La classe du point $\(\mathbf{x}\)$ est prédite par $\(\hat{y} = \text{signe}(f(\mathbf{x}))\)$ . 

Comment choisir C ?

Le paramètre de régularisation doit être déterminé par une procédure de sélection de modèle, par exemple par validation croisée (voir le chapitre "Bien apprendre, c'est généraliser : comprenez le principe de généralisation").

Apprenez une fonction de classification non-linéaire

Que se passe-t-il si nous devons classifier les données de la figure 5-a ?

Il est évident que nous ne pouvons pas trouver un modèle SVM linéaire capable de classer correctement ces points. Pourtant, nous voyons qu'une fonction de classification quadratique (une parabole) peut parfaitement séparer les deux classes.

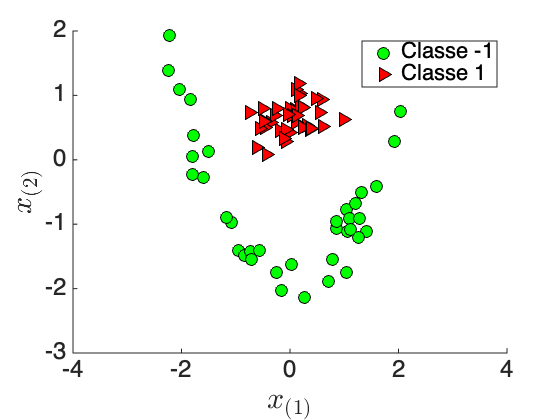
Figure 5-a : Données non linéairement séparables
Figure 5-a : Données non linéairement séparables

Pour cela, réalisons la projection des points en dimension 3 ( figure 5-b) par la fonction non-linéaire :

$\(\begin{eqnarray} \mathbb{R}^d & \longrightarrow & \mathcal{H} \\ & \mathbf{x} \longmapsto & \Phi(\mathbf{x}) = \begin{bmatrix} x_{(1)}^2 \\ x_{(2)}^2 \\ \sqrt{2} \,x_{(1)}\, x_{(2)} \end{bmatrix} \end{eqnarray}\)$

avec $\(x_{(j)}\)$ la jème variable du vecteur 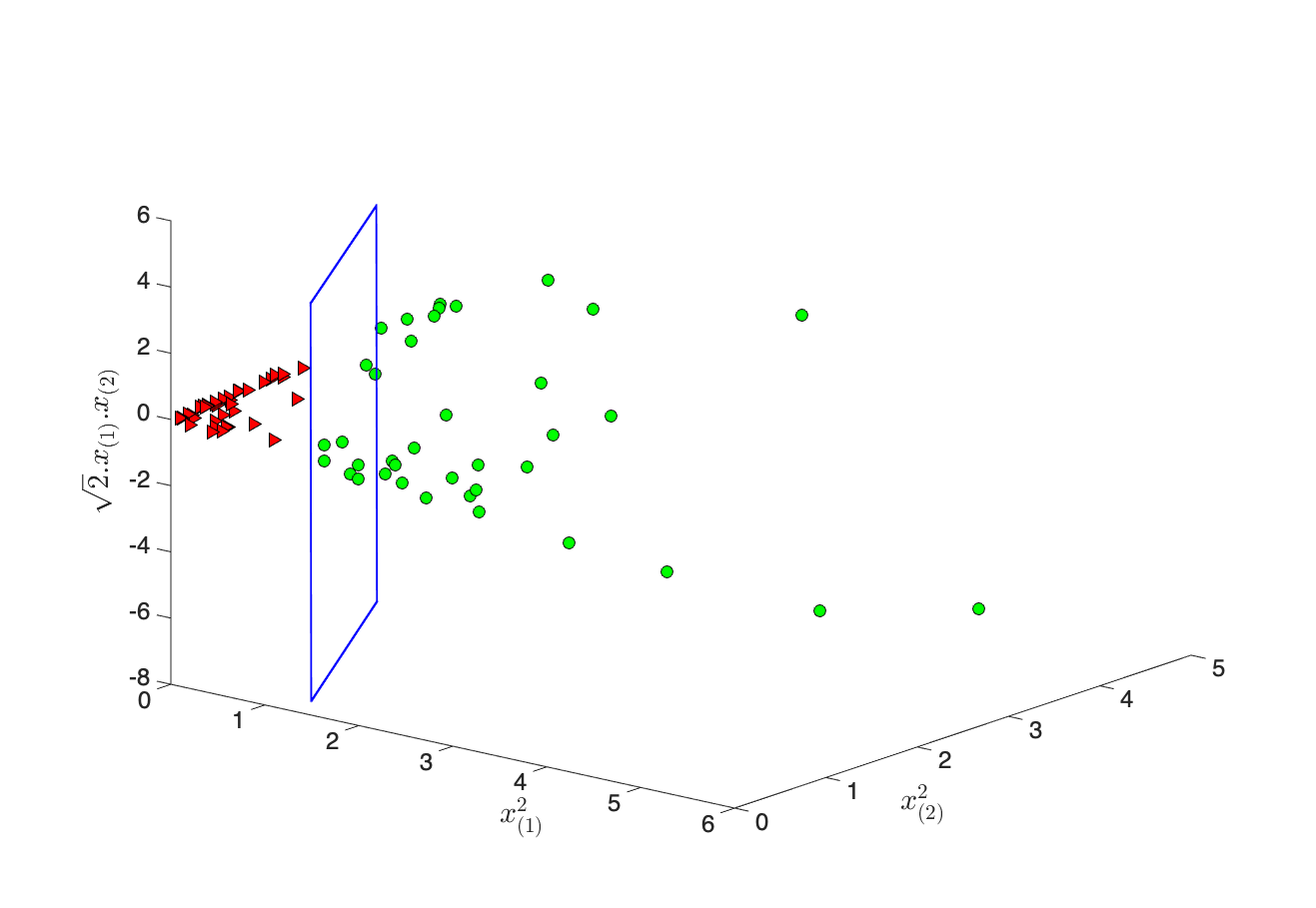$\(\mathbf{x}\)$ . Figure 5-b : Projection non-linéaire des pointsFigure 5-b : Projection non-linéaire des points. En bleu, la fonction de décision linéaire en 3D.

On peut apprendre avec les points $\(\{(\Phi(\mathbf{x}_i), y_i) \}_{i=1}^n\)$ un SVM linéaire    $\(f(\Phi(\mathbf{x})) = \boldsymbol{\beta}^\top\Phi(\mathbf{x}) + \beta_0\)$ (en bleu sur la figure 5-b) qui sépare correctement les deux classes. Dans l'espace d'origine $\(\mathbb{R}^2\)$ , la frontière de décision que nous obtenons est une fonction non-linéaire (figure 5-c) des points $\(\mathbf{x}\)$ .

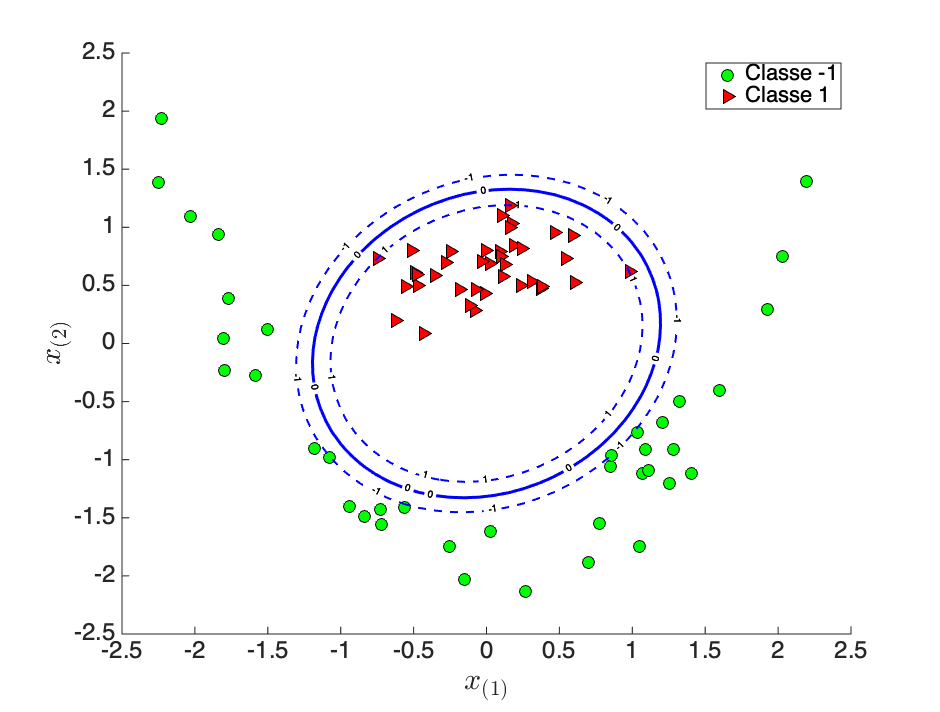
Figure 5-c : Fonction de décision non-linéaire
Figure 5-c : Fonction de décision non-linéaire

L'astuce du noyau

Qu'est-ce que cela change ?

Si nous adaptons le principe du SVM linéaire aux données  projetées  $\(\{(\Phi(\mathbf{x}_i), y_i) \}_{i=1}^n\)$ et apprenons un SVM, nous obtenons alors le modèle suivant :

$\[\begin{eqnarray} f(\mathbf{x}) & = & \sum_{i \in SV} \, \hat{\alpha}_i \, y_i \, \underbrace{\Phi({\mathbf{x}}_i)^{\top} \Phi({\mathbf{x}})}_{\text{Noyau} \, k(\mathbf{x}_i, \, \mathbf{x})} + \hat \beta_0 \hspace{120pt} (4) \end{eqnarray}\]$

L'élément clé est la fonction noyau $\(k(\mathbf{x}_i, \, \mathbf{x})= \Phi({\mathbf{x}}_i)^\top \Phi({\mathbf{x}})\)$ , qui permet d'obtenir la fonction de séparation non-linéaire (sans connaitre explicitement parfois la fonction de mapping $\(\Phi({\mathbf{x}})\)$ ).

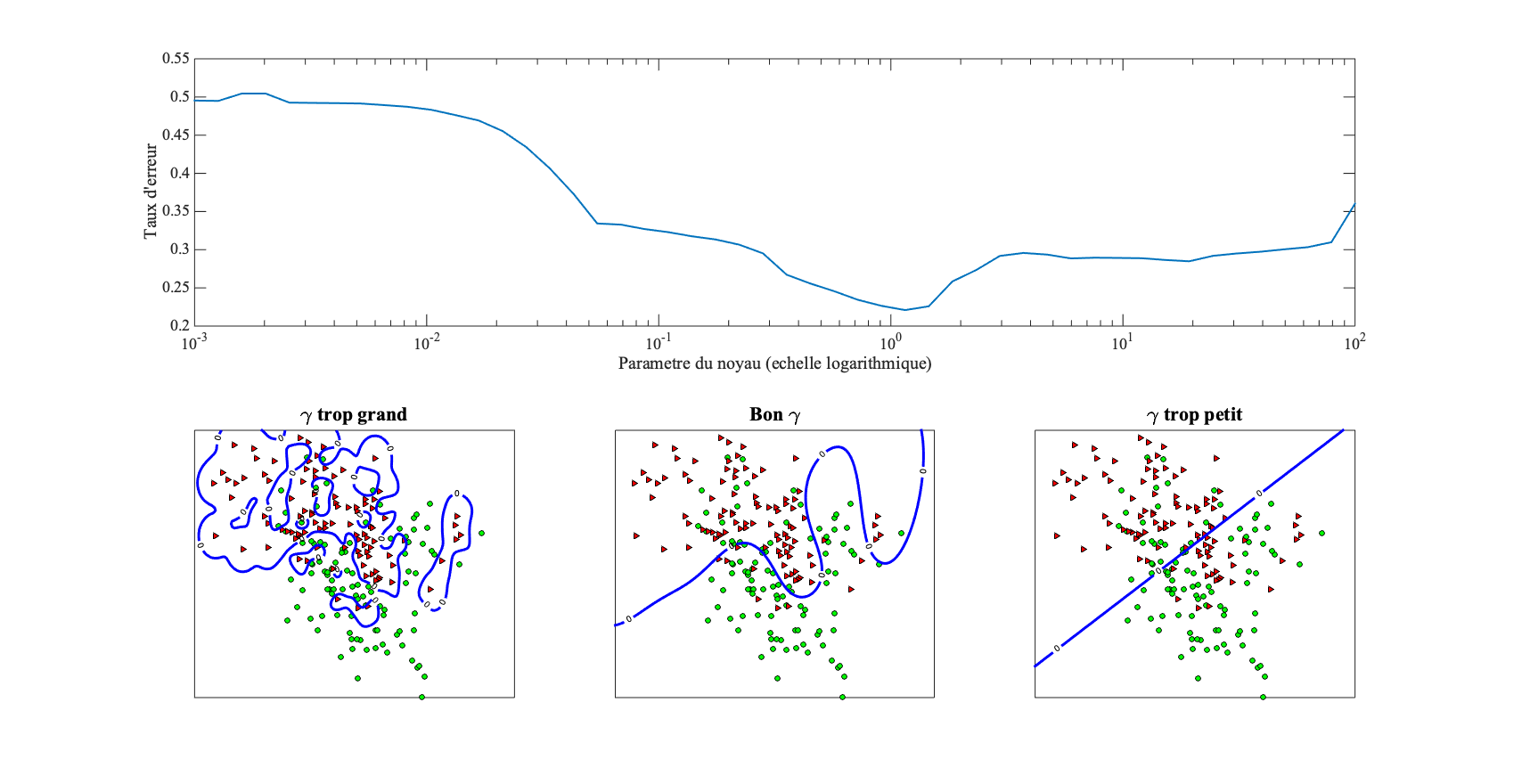
Réglez les paramètres de la fonction noyau

Le noyau dépend d'hyper-paramètres dont le réglage se fait par validation croisée comme pour $\(C\)$. La figure 6 analyse l'influence du paramètre du noyau sur la qualité de la fonction de classification en termes de frontière de séparation et du taux d'erreur sur des données de validation.

Figure 6 : influence du paramètre d'un noyau gaussien
Figure 6 : influence du paramètre d'un noyau gaussien. Sa "valeur optimale" est celle qui correspond au minimum de l'erreur de classification sur les données de validation. Le modèle associé est représenté au milieu en bas.

Généralisez le SVM au cas multi-classe

Comme pour la régression logistique, nous supposons $\(y \in {0, 1, \cdots, K-1}\)$  avec  $\(K > 2\)$ le nombre de classes.  Que ce soit en linéaire ou non-linéaire, nous pouvons passer du cas binaire au multi-classe par l'une des stratégies usuelles suivantes :

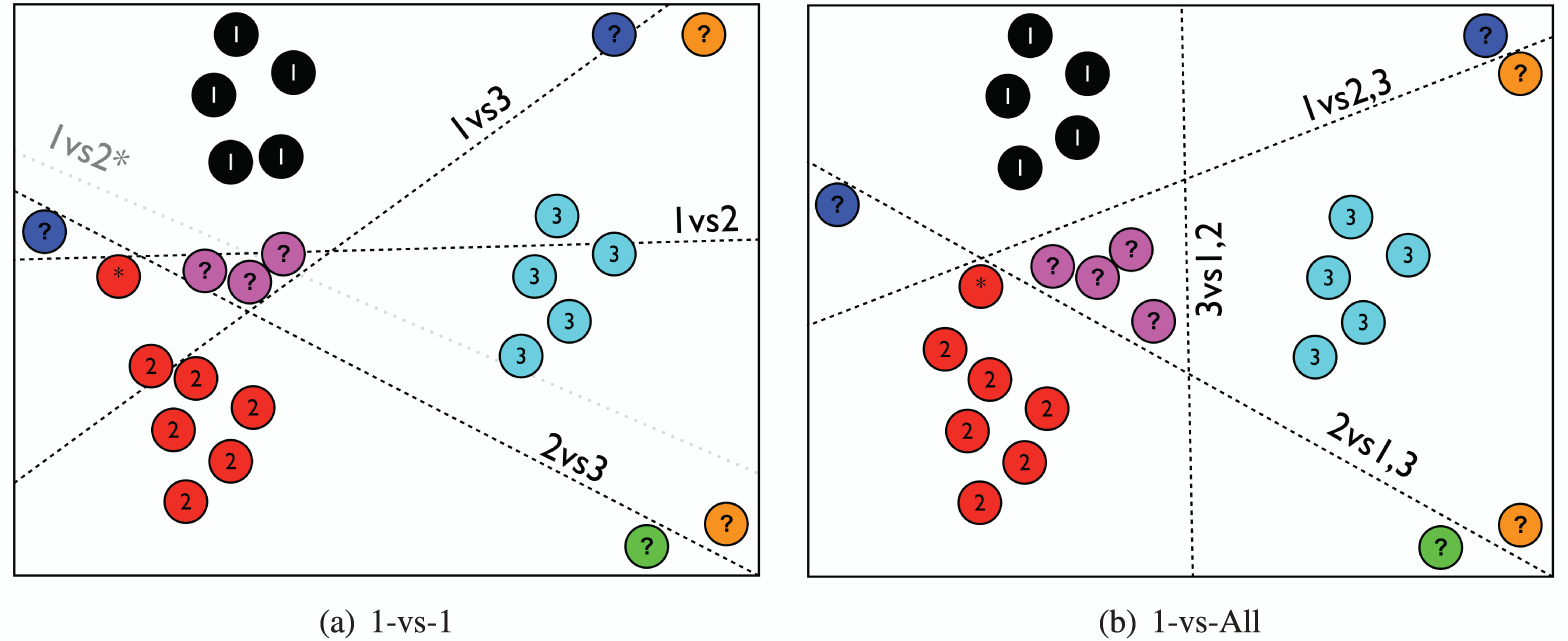
  • Un contre tous (one vs rest) : apprendre un SVM par classe (ladite classe contre les autres), calculer son score, et prédire la classe de score maximal (winner takes it all). Cela nécessite d'apprendre $\(K\)$ classifieurs.

  • Un contre un (one vs one) : apprendre autant de  classifieurs SVM que de paires de classes, prédire avec chaque classifieur et prédire la classe plébiscitée. On requiert $\(K(K-1)/2\)$ classifieurs.

La figure 7 montre les frontières de décision obtenues pour ces deux stratégies.

Figure 7 : stratégies de classification multi-classe
Figure 7 : stratégies de classification multi-classe (Source : W. Scheirer et al., "Towards Open Set Recognition", IEEE TPAMI, pp. 1757-1772, vol. 35, July 2013)

En résumé

Ce chapitre sur la méthode de classification SVM a permis :

  • de comprendre la notion de marge, qui sous-tend sa formulation,

  • d'appréhender le problème d'optimisation sous-jacent,

  • de se familiariser avec la notion de noyau, qui est un outil mathématique puissant pour étendre au cas non-linéaire une fonction de classification linéaire,

  • de savoir comment généraliser le concept aux problèmes de classification multi-classe.

Une question non abordée dans le chapitre est le choix de la fonction noyau. Notez qu'il existe de nombreux travaux scientifiques sur la construction de noyaux adaptés à un problème donné. De plus, l'utilisation de ces noyaux permet de réaliser la classification de données complexes comme les graphes, les histogrammes ou les séries temporelles.

Dans le prochain chapitre , nous allons  analyser la complexité algorithmique des différentes méthodes d'apprentissage statistique étudiées et leur passage à l'échelle pour traiter de grandes quantités de données.

Example of certificate of achievement
Example of certificate of achievement