• 12 hours
  • Medium
License

Free online content available in this course.

course.header.alt.is_video

course.header.alt.is_certifying

Got it!

Last updated on 1/29/24

Appréhendez la régression linéaire

L'objectif de ce chapitre est de :

  • comprendre la régression linéaire,

  • savoir expliquer le résultat de la régression linéaire,

  • déterminer les variables explicatives les plus pertinentes.

Il fait beau, mes vélos seront-ils loués ?

Prenons les données quotidiennes de location de vélos dans une ville américaine (un extrait est sur la figure ci-dessous). Elles peuvent être téléchargées  ici. 

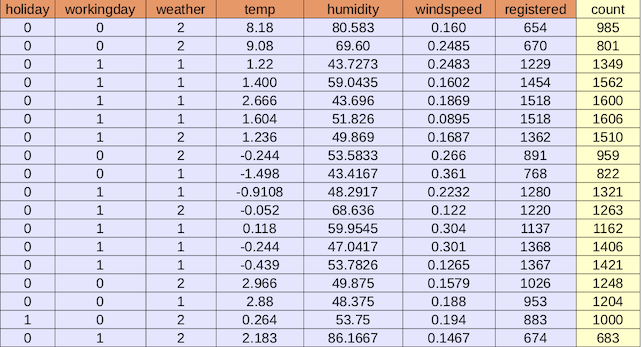
Données location de vélos
Tableau 1 : Données location de vélos

L'objectif est de prédire le nombre de locations (la colonne count)  en utilisant les autres variables. La signification des variables est présentée dans le tableau 2.

Variable

holiday

workingday

weather

temp

humidity

windspeed

registered

count

Signification

jour férié

jour ouvré

météo

température

humidité

vitesse du vent

nombre d'abonnés

nombre de locations

Nature

 binaire

binaire

catégorielle

continue

 continue

 continue

continue

 continue

Tableau 2 :  signification et nature des variables

Comme dans le cours sur l'ACP, nous allons noter $\(\mathbf{X} \in \mathbb{R}^{n \times d}\)$ la matrice des données sans la colonne count. $\(n\)$ est le nombre de données et $\(d\)$ le nombre de variables.

Définissez un modèle de régression linéaire

Régression mono-variable

Prédisons les locations de vélos en fonction de la température :

$\(count = \beta_1 \times temp + \beta_0 + e\)$

 $\(e\)$ représente l'écart entre la prédiction  $\( \beta_1 \times temp + \beta_0\)$  et la vraie valeur $\(count\)$ comme le montre la figure 1.

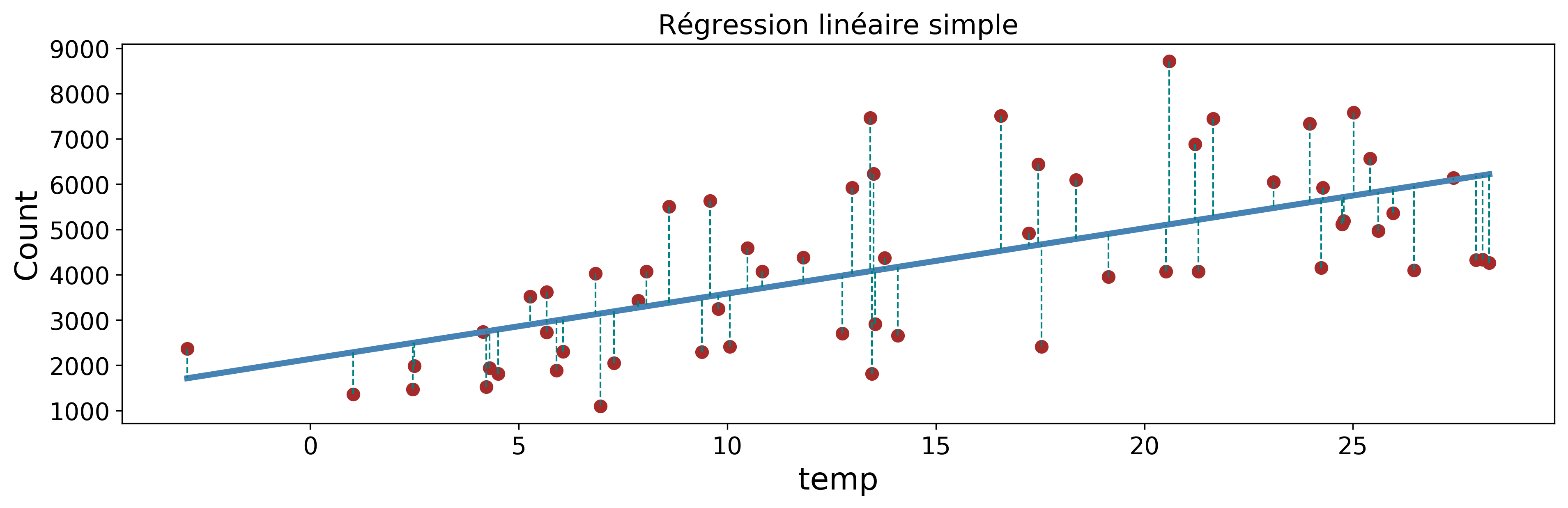
Droite de régression linéaire. Les points rouges sont les données ; les erreurs sont matérialisées par les lignes en pointillé
Figure 1 : Droite de régression linéaire. Les points rouges sont les données ; les erreurs sont matérialisées par les lignes en pointillé.

Les paramètres  $\(\beta_1\)$ et  $\(\beta_0\)$ sont déterminés de façon à minimiser ces erreurs.

Régression multiple

Pour la suite, utilisons la terminologie suivante :

  • count : sortie ou variable à prédire notée $\(y\)$ ,

  • holiday, ..., temp, ..., registered (nombre d'abonnés) : entrées ou variables prédictives. Notons $\(\mathbf{x} \in \mathbb{R}^d\)$   le vecteur contenant ces variables.

Le modèle de régression est maintenant

$\[y = \beta_0 + \beta_1 \times holiday + \cdots + \beta_d \times registered + e = \beta_0 + \mathbf{x}^\top \boldsymbol{\beta} + e\]$

 avec $\(\beta_0\)$ l'ordonnée à l'origine et  $\(\boldsymbol{\beta} \in \mathbb{R}^d\)$ le vecteur de paramètres associé aux entrées.

Comment déterminer les paramètres du modèle  ?

Par minimisation du critère des moindres carrés :

avec les définitions suivantes :

$\(\quad \boldsymbol{\beta}_a = \begin{bmatrix} \beta_0 \\ \boldsymbol{\beta} \end{bmatrix} \in \mathbb{R}^{d+1}\, , \,\,\, \mathbf{X}_a = \begin{bmatrix} \boldsymbol{1} & \mathbf{X} \end{bmatrix} \in \mathbb{R}^{n \times (d+1)}\)$

 $\(\mathbf{Y} = \begin{bmatrix} y_1 \\ \vdots \\ y_n \end{bmatrix} \in \mathbb{R}^n\)$ est le vecteur des sorties, $\(\mathbf{1} = \begin{bmatrix} 1 \\ \vdots \\ 1 \end{bmatrix} \in \mathbb{R}^n\)$   est un vecteur de 1 et

$\(\mathbf{X} = \begin{bmatrix} x_{1,1} & x_{1,2} & \cdots & x_{1,d} \\ x_{2,1} & x_{2,2} & \cdots & x_{2,d} \\ \vdots & \vdots & \vdots & \vdots \\ x_{n,1} & x_{n,2} & \cdots & x_{n,d} \end{bmatrix} \in \mathbb{R}^{n \times d}\)$ est la matrice contenant les variables prédictives.

Comment juger de la qualité du modèle ?

  • Comparez visuellement les prédictions  $\(\hat y = \hat{\beta}_0 + \mathbf{x}^\top \hat{ \boldsymbol{\beta}}\)$ et les vraies observations $\(y\)$ (figure 2).

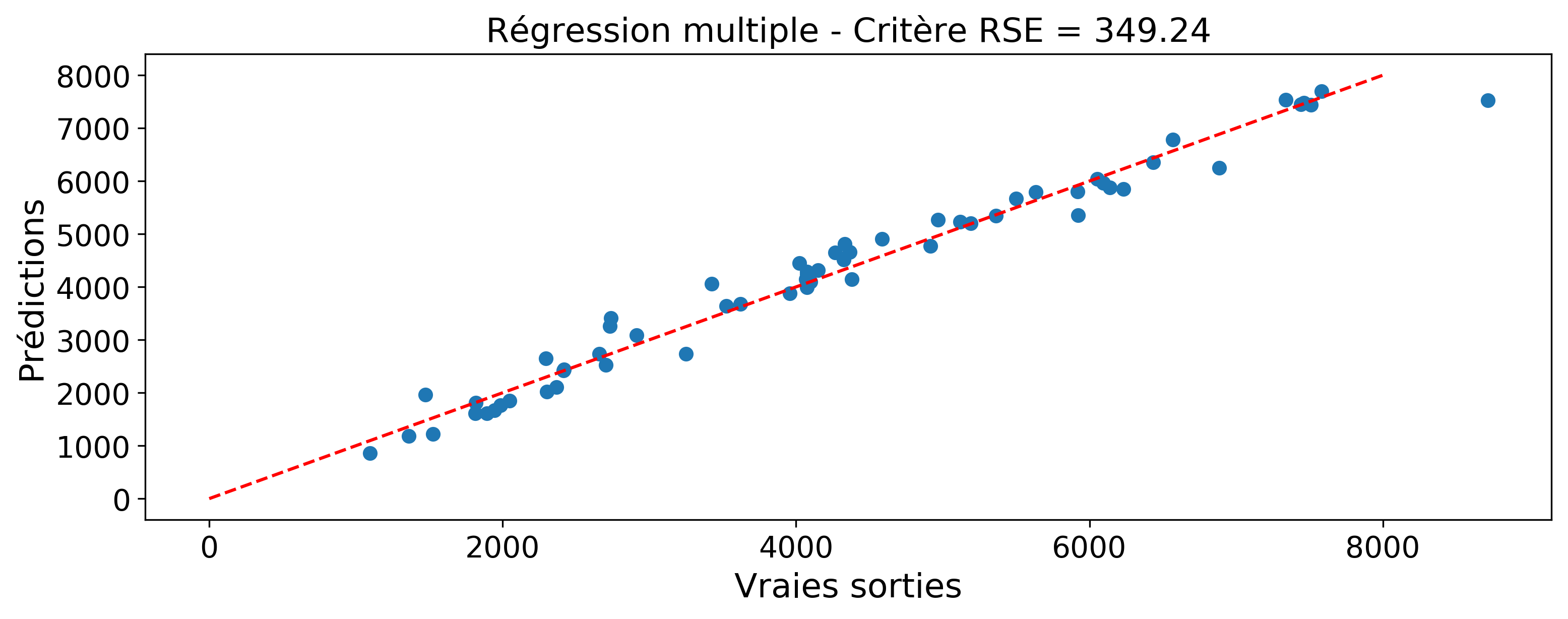
Tracé des vraies observations en fonction des prédictions. La droite en pointillé représente la prédiction idéale.
Figure 2 : Tracé des vraies observations en fonction des prédictions. La droite en pointillé représente la prédiction idéale.

  •  Évaluez l'erreur de prédiction :

$\[RSE = \sqrt{\frac{1}{n-d-1} \sum_{i=1}^n (y_i - \hat{y}_i)^2}\]$

Plus ce critère est petit, mieux c'est.

Sélectionnez les variables explicatives

A-t-on besoin de toutes les variables holiday, ..., temp, ..., registered ?

Pour sélectionner les variables pertinentes parmi les  $\(d\)$  disponibles, plusieurs stratégies sont possibles :

  • Meilleur sous-ensemble : il faut tester tous les modèles linéaires possibles à 1 variable,  puis 2 variables et ainsi de suite. Cela nécessite d'explorer $\(2^d\)$ possibilités. Cette méthode a une complexité exponentielle par rapport au nombre de variables $\(d\)$ .

  • Forward Selection : on inclue une à une les variables dans le modèle, soit $\(\mathcal{O}(d^2)\)$ possibilités.

  • Backward Selection : partant d'un modèle incluant toutes les variables, on retire à chaque étape une variable, soit aussi $\(\mathcal{O}(d^2)\)$ possibilités.

  • Pénaliser les paramètres : deux variantes sont la régression ridge et le lasso.

Régression linéaire pénalisée

Elle consiste à déterminer les paramètres par minimisation du critère des moindres carrés régularisé :

$\[\min_{\beta_0, \, \boldsymbol{\beta}} \,\, \frac{1}{2} \sum_{i=1}^n \left(y_i - \beta_0 - \boldsymbol{x}_i^\top \boldsymbol{\beta} \right)^2 + \lambda \, \Omega(\boldsymbol{\beta})\hspace{84pt} (3)\]$

  $\(\lambda \geq 0\)$ est le paramètre de régularisation (à choisir par l'utilisateur) et  $\(\Omega(\boldsymbol{\beta}) \geq 0\)$ est le terme de régularisation.

L'idée ici est de pousser certains paramètres  $\(\beta_j\)$ (ceux qui sont associés aux variables explicatives qui ne sont pas essentielles pour décrire la sortie $\(y\)$ ) en jouant sur la valeur de  $\(\lambda\)$ et la forme de $\(\Omega(\boldsymbol{\beta})\)$ . À l'extrême, lorsque :

  •  $\(\lambda \rightarrow \infty\)$ on souhaite avoir  $\(\Omega(\boldsymbol{\beta}) \rightarrow 0\)$ c'est-à-dire $\(\boldsymbol{\beta} = \boldsymbol{0}\)$ (aucune variable n'est sélectionnée) ;

  •  $\(\lambda = 0,\)$ nous retrouvons la solution (2) de la régression linéaire (toutes les variables explicatives sont incluses dans le modèle).

Les choix appropriés de $\(\lambda\)$ et  $\(\boldsymbol{\beta}\)$ permettront de déterminer un compromis entre ces deux situations extrêmes.

On remarquera que le paramètre $\(\beta_0\)$ (la coordonnée à l'origine) n'est pas pénalisée.

Influence de la régularisation

Pour mieux comprendre comment ces méthodes de régularisation agissent, considérons cet exemple simple. Supposons qu'on dispose d'une seule observation  $\(y \in \mathbb{R}\)$ et qu'on cherche le modèle $\(y = \beta + e \)$ avec $\(\beta \in \mathbb{R}\)$ . Les deux fonctions de régularisation sont représentées sur la figure 3.

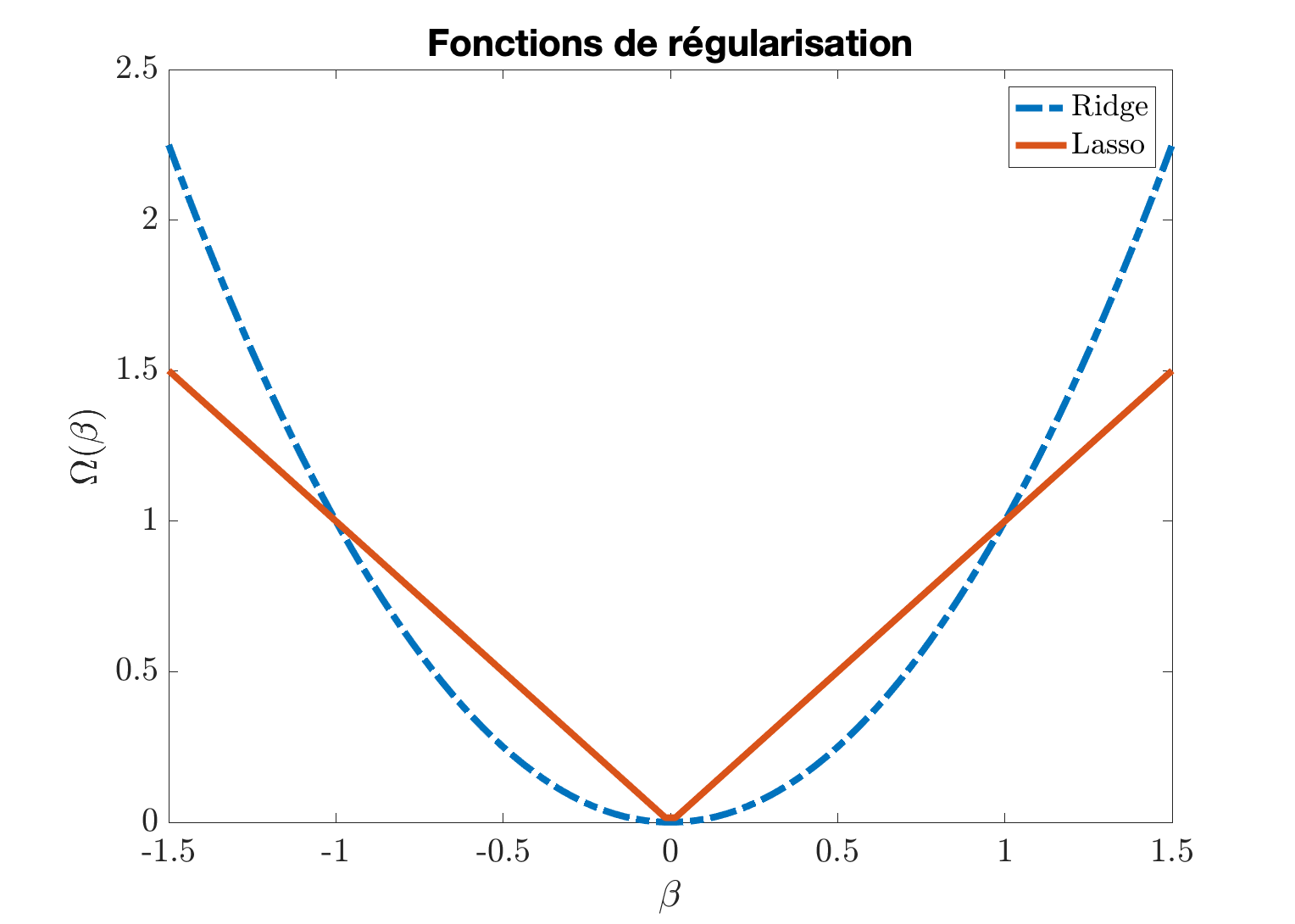
Figure 3 : fonctions de régularisation ridge et lasso
Figure 3 : fonctions de régularisation ridge et lasso

  • Pour la régression ridge, nous avons à résoudre

$\[\min_{\beta} \,\, \frac{1}{2} (y - \beta)^2 + \lambda \, \beta^2\]$

La condition d'optimalité (annulation du gradient) fournit la solution

$\[\hat{\beta} = \frac{y}{1 + \lambda}\]$

Nous constatons que $\(\hat{\beta} \longrightarrow 0 \)$  si  $\(\lambda \longrightarrow \infty\)$ .

  • Le problème du lasso s'écrit

$\(\min_{\beta} \,\, \frac{1}{2} (y - \beta)^2 + \lambda \, |\beta|\hspace{84pt} (4)\)$

La difficulté du lasso est la non-dérivabilité de la fonction $\(|\beta|\)$ en 0 (voir figure 3). Néanmoins on a :

  • pour $\(\beta \rightarrow 0^+\)$ la dérivée est $\(g^+= -y + \lambda\)$ ,

  • pour  $\(\beta \rightarrow 0^-\)$ la dérivée est $\(g^-= -y - \lambda\)$ .

La condition d'optimalité s'écrit alors :

  • si  $\(\beta \neq 0\)$ on a $\( -(y - \beta) + \lambda \, \text{signe}(\beta) = 0\)$ ,

  • si  $\(\beta = 0\)$ on a $\(g^+ \geq 0\)$ et $\(g^- \leq 0\)$ .

Nous en déduisons pour le problème (4) une solution analytique sous la forme :

$\[\hat{\beta} = \left \lbrace \begin{array}{lll} y + \lambda & \text{si} & y \leq - \lambda \\ 0 & \text{si} & -\lambda \leq y \leq \lambda \\ y - \lambda & \text{si} & y \geq \lambda \end{array} \right.\hspace{84pt} (5)\]$

La figure 4 montre l'influence des deux formes de régularisation.

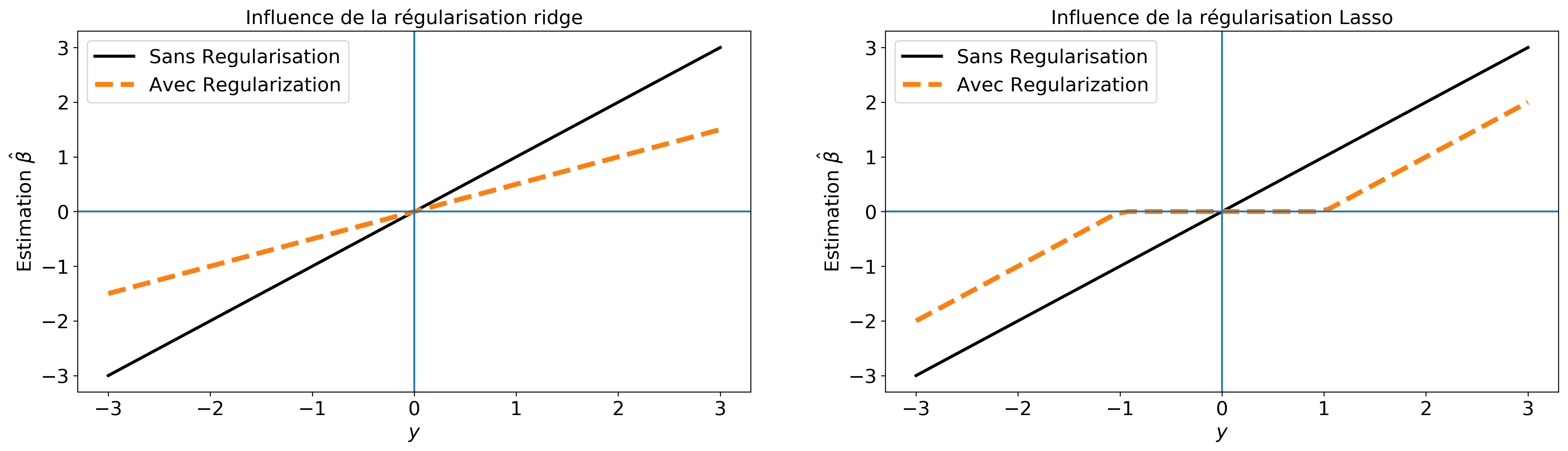
Illustration de l'effet de rétrecissement des paramètres effectué par les régularisation ridge et lasso.
Figure 4 : Illustration de l'effet de rétrécissement des paramètres dû aux régularisations ridge et lasso. Courbes tracées pour \(\lambda = 1\) .
Solution de la régression linéaire pénalisée

Revenons maintenant à notre problème général (équation 3).

On peut montrer que le problème de régression ridge admet une solution analytique. En effet, si nous écrivons la condition d'optimalité respectivement par rapport à $\(\beta_0\)$ et $\(\boldsymbol{\beta}\)$ nous obtenons

$\[\hat{\beta_0} = \bar{y} - \bar{\mathbf{x}}^\top\hat {\boldsymbol{\beta}} \quad \text{et} \quad \hat {\boldsymbol{\beta}} = \left(\mathbf{X}_c^\top \mathbf{X}_c + \lambda \, \mathbf{I} \right)^{-1} \left( \mathbf{X}_c^\top \mathbf{Y}_c \right) \hspace{84pt} (4)\]$

avec  $\(\bar{y}\)$ la moyenne des sorties,  $\(\bar{\mathbf{x}}\)$ la moyenne des variables explicatives,   $\(\mathbf{X}_c\)$  la matrice des données centrées,  $\(\mathbf{Y}_c = \mathbf{Y} - \bar{y}\)$ le vecteur des sorties centrées et   $\(\mathbf{I} \in \mathbb{R}^{d \times d}\)$ la matrice identité. L'expression de cette solution est presque similaire à celle de la régression linéaire (voir équation 2) au terme  $\(\lambda \, \boldsymbol{I}\)$ près.

Pour la régression lasso, la solution $\(\hat{\beta}_0\)$ est la même que celle de la régression ridge. En revanche, $\(\hat{\boldsymbol{\beta}}\)$ n'admet pas de solution analytique et se détermine via des algorithmes d'optimisation itératifs. Un exemple d'algorithme de résolution du problème lasso est le suivant :

  • Initialisation

    •  $\(\text{centrer les sorties} \,\, y_i \longleftarrow y_i - \bar{y} \,\, \text{et les entrées} \,\, \mathbf{x}_i - \bar{\mathbf{x}} \,\, \forall i=1, \cdots, n\)$

    •  $\(\text{fixer} \,\; {\boldsymbol{\beta}}^0 = \boldsymbol{0}, \,\, \text{et} \,\, t=0\)$

  • Répétez

    •   $\({\color{magenta}{\beta}_1^t } \longleftarrow \arg\min{\color{red} \beta_1} \,\, \sum_{i=1}^n \left(y_i - {\color{red} x_{i1} \, \beta_1} - \sum_{j \neq 1}\, \, x_{ij} \,\ \color{blue}\beta_j^{t-1} \,\, \right)^2 + \lambda \,\, {\color{red} |\beta_1|}\)$  

    •   $\({\color{magenta} {\beta}_2^t } \longleftarrow \arg\min{\color{red} \beta_2} \,\, \sum_{i=1}^n \left(y_i- {\color{magenta} x_{i1} \, \beta_1^t} - {\color{red} x_{i2} \, \beta_2}- \sum_{j=3}^d\, \, x_{ij} \,\ \color{blue}\beta_j^{t-1} \,\,\right)^2 + \lambda \,\, {\color{red} |\beta_2|}\)$

    •  $\(\vdots\)$

    •  $\({\color{magenta}{\beta}_d^t } \longleftarrow \arg\min{\color{red} \beta_d} \,\, \sum_{i=1}^n \left(y_i - \sum_{j =1}^{d-1}\, \, x_{ij} \,\ \color{magenta}\beta_j^{t} \right)^2 + \lambda \,\, {\color{red} |\beta_d|}\)$

    •  $\(t \leftarrow t+1\)$

  • Jusqu'à convergence

  • Calculez $\(\beta_0 \leftarrow y - \bar{\mathbf{x}}^\top\boldsymbol{\beta}\)$

Le principe est qu'à chaque itération, on fixe tous les paramètres $\(\beta_j\)$ sauf un, dont on optimise la valeur en résolvant un problème de lasso simplifié comme à l'équation (4).  Sa solution s'obtient par une opération de seuillage doux. Cette procédure est répétée jusqu'à la convergence des paramètres $\(\boldsymbol{\beta}\)$ .

Notez qu'il existe des boîtes à outils comme sklearn ou CVX qui implémentent la solution de la régression lasso.

Réglage du paramètre de régularisation $\(\lambda\)$ 

Comment sélectionner le bon paramètre de régularisation ?

Les figures 5 et 6 montrent l'effet de la régularisation en fonction de  $\(\lambda\)$ .

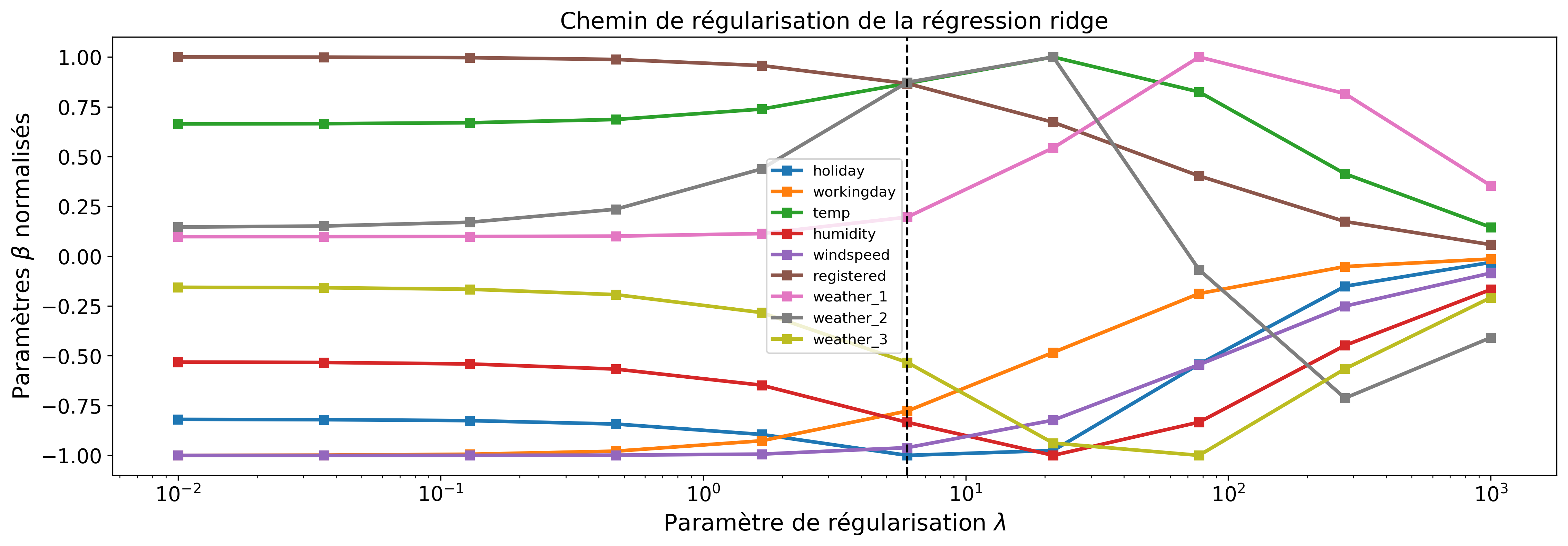
Chemin de régularisation pour la régression ridge. Pour faciliter la visualisation, nous avons tracé les paramètres normalisés
Figure 5 : Chemin de régularisation pour la régression ridge. Pour faciliter la visualisation, nous avons tracé les paramètres normalisés.
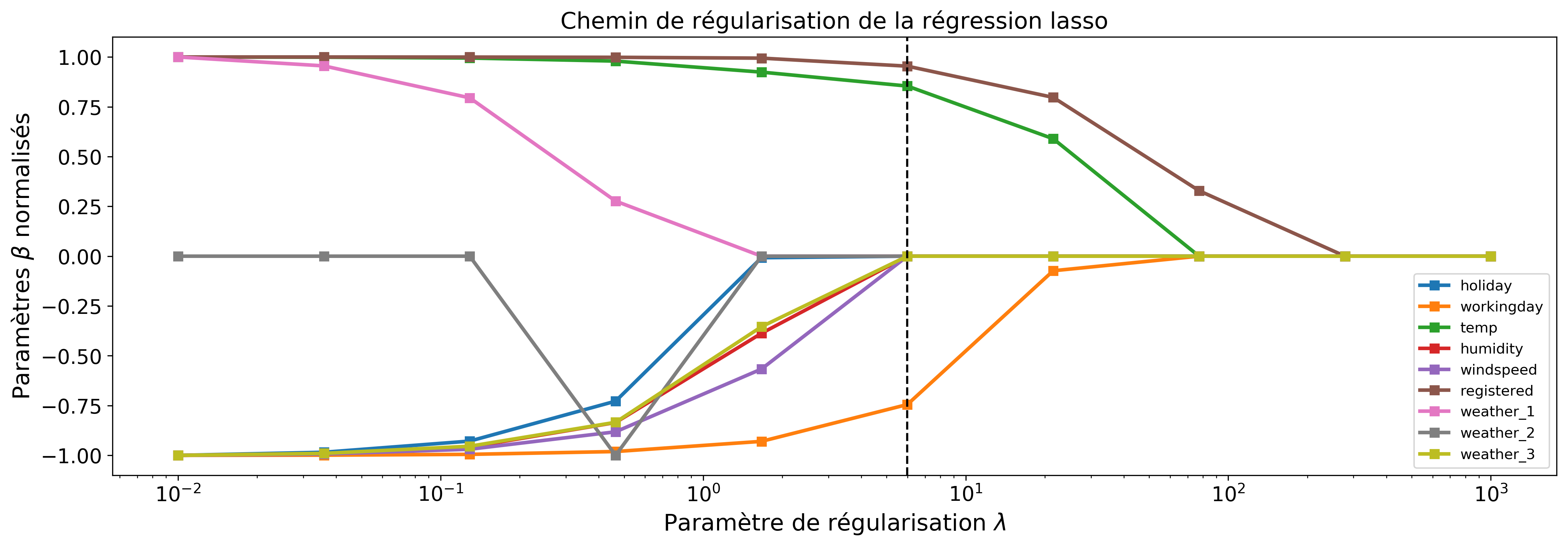
Chemin de régularisation de la régression lasso
Figure 6 : Chemin de régularisation de la régression lasso

En pratique, on teste différentes valeurs de $\(\lambda\)$ (souvent prises sur une échelle logarithmique) et on évalue à chaque fois le modèle obtenu. Nous pouvons nous servir du critère RSE calculé sur les données de validation (toujours cette notion de généralisation du modèle) pour sélectionner alors le $\(\lambda\)$ "optimal". Le graphique de la figure 7 montre la courbe de validation pour le lasso.

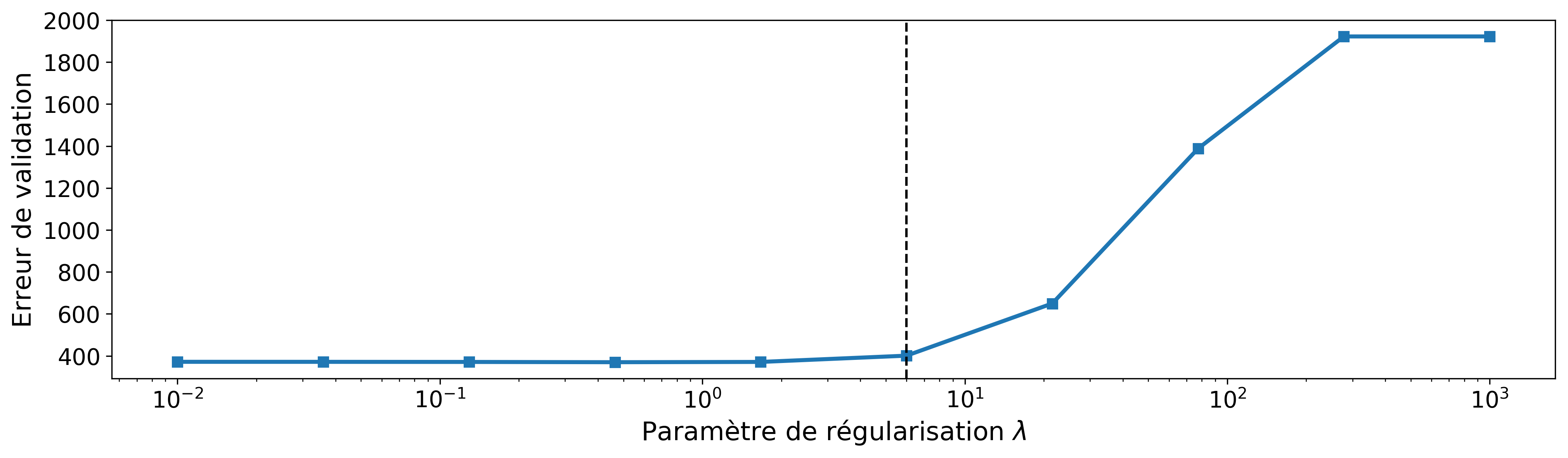
Critère de validation en fonction du paramètre de régularisation pour le lasso. La ligne en pointillé indique la valeur que nous avons retenue.
Figure 7 : Critère de validation en fonction du paramètre de régularisation pour la régression lasso. La ligne en pointillé indique la valeur retenue.

En se reportant au graphique du chemin de régularisation, nous constatons que pour la valeur de $\(\lambda\)$ retenue, seules les variables "workingday", "temp" et "registered" sont sélectionnées. (Ceci signifie que les locations journalières de vélos peuvent s'expliquer par la température, le nombre d'abonnés au service de location et au fait que la journée soit ouvrée ou non.)

En résumé

Dans ce chapitre, vous avez appris :

  • comment construire un modèle de régression linéaire,

  • comment qualifier ses performances,

  • comment sélectionner les variables pertinentes en utilisant notamment le lasso.

Dans le prochain chapitre, nous verrons comment passer de la régression linéaire à la régression logistique.

Example of certificate of achievement
Example of certificate of achievement