Initiez-vous au Machine Learning

Découvrez les différents types de modèles

Découvrons plus précisément ce que l'on entend par modèle prédictif. Il existe une multitude de types de modèles, chacun avec son histoire, ses caractéristiques et ses performances propres.

Ne pouvant tous les tester un par un, vous devez pouvoir choisir rapidement comment vous équiper au mieux pour apprivoiser votre dataset.

En règle générale, vous choisirez le modèle en fonction du contexte et du cahier des charges du projet :

• la tâche à effectuer : régression, classification ou clustering ;

• la nature des données : chiffres, catégories, texte, images, vidéo, sons, séries temporelles ;

• le volume des données ;

• les caractéristiques statistiques des données : linéarité, stationnarité, amplitude, complétude, cohérence, etc.

Pour gagner du temps, on distingue de nos jours les classes principales suivantes :

1. Les modèles de régression

2. Les modèles à base d'arbres

3. Les réseaux de neurones et le Deep Learning

Les modèles de régression 

Adaptés à des jeux de données de taille limitée où les relations entre les variables sont linéaires, au moins jusqu'à un certain point. On parle aussi de Generalized Linear Model (GLM), famille de modèles qui comprend la régression linéaire sous toutes ses formes mais aussi des variantes pour la classification.

On parle de modèles de régression mais cela ne veut pas dire qu'ils soient limités aux problèmes de régression ! Comme nous le verrons dans la partie 2, les modèles de régression peuvent être utilisés pour résoudre à la fois des problèmes de régression (prédiction de valeurs continues) et des problèmes de classification (prédiction de catégories discrètes).

Les modèles à base d'arbres 

Arbre de décision (decision tree), forêt aléatoire (random forest), ainsi que XGBoost et ses nombreuses variantes, ces modèles sont adaptés à des jeux de données tabulaires de taille plus conséquente. Ils sont très robustes face aux données manquantes et aux observations aberrantes (outliers, en anglais). Ce sont de loin les grands gagnants des compétitions Kaggle adaptées.

Les réseaux de neurones et le Deep Learning

Adaptés à des jeux de données de gros volume, de nature plus complexe, comme des images ou de la vidéo. Bien plus polyvalents dans la nature des données prises en compte (images, vidéo), ils offrent des gains de performances significatifs lorsqu’appliqués à de gros volumes de données.

Les autres types de modèles, bien que sûrement pertinents dans des contextes bien particuliers, n'auront pas la polyvalence et la robustesse offerte dans ces 3 types de modèles.

Sachez définir un modèle

Mais de quoi parle-t-on au juste quand on parle de modèle ?

On va distinguer :

• le type de modèle : XGBoost, NN, LR : il s'agit là de la méthode issue d'un raisonnement mathématique et traduite en code ;

• de son instanciation après entraînement du modèle sur les données. 

Le type de modèle

En Python on importe le modèle en tant que librairie.

Exemple avec le modèle de régression linéaire :

from sklearn.ensemble import LinearRegression

L’instanciation du modèle après entraînement

En Python, cela consiste à utiliser la méthode  fit()  :

# Soit des données artificielles
X = [[0, 0], [1, 1]]
y = [0, 1]
# la classe du modèle
from sklearn.ensemble import LinearRegression
# l'instanciation du modèle
mdl = LinearRegression()
mdl = mdl.fit(X, y)

Dans le code ci-dessus,  clf  est le modèle instancié, qui est entraîné sur les données  X  et  y  .

Par souci de simplicité on parlera de modèle dans les 2 cas, classe et instance, mais il est bon de souligner la différence.

Sachez définir un algorithme

Je voudrais illustrer par un exemple ce qu'est un algorithme d'entraînement, de façon à faire jaillir une notion fondamentale du Machine Learning : l'erreur d'estimation !

Un algorithme est une série d'instructions définies et ordonnées qui permettent d'effectuer une tâche spécifique, un calcul par exemple. L'idée est de répéter une tâche facile et simple pour réaliser en fin de compte une tâche plus complexe.

Prenons donc un exemple d'algorithme avec le calcul de la racine de 2.

Partons d'une valeur candidate (x = 1) et mettons à jour cette valeur jusqu'à ce que le résultat soit assez proche du résultat attendu.

On saura si x est proche de la racine carrée de 2, si on a x^2 proche de 2.

Voici donc l'algorithme de Héron pour le calcul des racines carrées :

1. Soit une valeur d'initialisation pour $\$\backslash (x\; :\; x\; =\; 1\backslash )\$$ 

2. Fixons la précision attendue : précision = $\$\backslash (0,001\backslash )\$$ 

3. Tant que |x^2 - 2| > précision

 $\$\backslash (x\; =\; (x\; +\; 2/x)/2\backslash )\$$

Si la différence entre $\$\backslash (x^2\backslash )\$$ et $\$\backslash (2\backslash )\$$ est supérieure à la précision que nous avons fixée, nous itérons via la formule x = (x + 2/x)/2 en donnant à $\$\backslash (x\backslash )\$$ une nouvelle valeur. Sinon, nous avons notre approximation finale et nous pouvons nous arrêter.

Demandons à chatGPT de mieux nous l'expliquer :

Chercher à savoir quelle est la racine carrée de 2, c'est comme chercher un nombre que l'on peut multiplier par lui-même pour obtenir 2. Cette méthode nous permet de trouver une réponse proche de la vraie valeur en effectuant quelques calculs simples.

Voici comment ça fonctionne :

On commence avec une valeur initiale pour x, disons x = 1.

On décide de la précision que l'on souhaite atteindre. Par exemple, précision = 0,001. Cela signifie que l'approximation que nous trouverons sera correcte jusqu'à trois décimales après la virgule.

Ensuite, nous allons répéter les étapes suivantes jusqu'à ce que notre approximation soit assez proche de la racine carrée de 2 :

• On calcule $\$\backslash (x^2\backslash )\$$

• On compare cette valeur avec $\$\backslash (2\backslash )\$$

• Si la différence entre $\$\backslash (x^2\backslash )\$$ et  $\$\backslash (2\backslash )\$$   est supérieure à la précision que nous avons fixée, nous continuons le processus.

• Sinon, nous avons notre approximation finale et nous pouvons nous arrêter.

L'étape cruciale de l'algorithme est la mise à jour de la valeur de x à chaque itération. On la calcule en utilisant la formule suivante :

 $\$\backslash (x\; =\; (x\; +\; 2/x)\; /\; 2\backslash )\$$

Cette mise à jour permet d'approcher de plus en plus la racine carrée de 2 à chaque itération, jusqu'à ce que la précision souhaitée soit atteinte.

En résumé, l'algorithme de Héron nous permet de trouver une approximation de la racine carrée de 2 en utilisant des calculs simples, et nous nous arrêtons lorsque notre résultat est suffisamment proche de la vraie valeur.

En Python cela s'écrit :

# initialisation
x = 1
precision = 0.001
# boucle itérative
while (abs(x**2 - 2) > precision) :
    x = (x + 2/x)/2

print(x)

Cet algorithme est extrêmement efficace. En seulement trois étapes, la précision relative sur la valeur de √2 est déjà de 10–6, ce qui est excellent, et de moins de 10–12 en quatre étapes.

Remarquez maintenant la quantité $\$\backslash (|x^2\; -\; 2|\backslash )\$$  que nous avons calculée à chaque itération : la différence en valeur absolue entre la valeur candidate au carré $\$\backslash (x^2\backslash )\$$  et 2. C'est l'erreur d'estimation entre la valeur estimée et la valeur dite de vérité (groundtruth, en anglais). On peut réécrire l'algorithme en mettant en avant cette erreur d'estimation :

# initialisation
x = 1
erreur = 1
précision = 0.001
# boucle itérative
Tant que erreur > précision:
    # mise à jour de l'estimation
    x = (x + 2/x)/2
    # mise à jour de l'erreur avec la nouvelle valeur de x
    erreur = |x^2 - 2|

Voilà ! Dans cet algorithme qui date de presque 2 000 ans, nous avons les composantes principales d'un algorithme de Machine Learning :

• la notion d'erreur d'estimation :  erreur = |x^2 - 2|

• la mise à jour itérative de l'estimation :  x = (x + 2/x)/2

Note : au lieu de calculer la valeur absolue de l'erreur d'estimation, nous aurions pu aussi prendre son carré au lieu de sa valeur absolue. Nous aurions eu l'algorithme suivant avec une estimation de l'erreur appelée Root Mean Square Error ou RMSE pour les intimes.

Tant que erreur > precision:
    # màj de l'estimation
    x = (x + 2/x)/2
    # mise à jour de l'erreur avec la nouvelle valeur de x
    erreur = sqrt(x^2 - 2)^2

La question est alors de savoir si ce critère fait converger plus ou moins rapidement l'estimation de la racine de 2. Qu'en pensez-vous ?

Un algorithme en particulier est communément utilisé pour entraîner les modèles de ML, Deep Learning inclus. Il s'agit du gradient stochastique. Sans rentrer dans les détails, le gradient stochastique fonctionne presque comme l'algorithme de Héron. En voici une version simplifiée :

Soit un jeu d'échantillons, on cherche à estimer un vecteur h qui minimise un critère que l'on appelle une fonction de coût.

On se dote d'un paramètre essentiel, le learning rate ou taux d'apprentissage, qui va permettre de régler l'intensité de la correction de l'estimation apportée par l'erreur d'estimation. Le learning rate est en quelque sorte un gros bouton qui permet d'ajuster la vitesse de mise à jour de l'estimation et donc la vitesse de convergence de l'algorithme. On le note en général .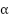

On aura, de façon simplifiée, à chaque itération :

• calcul de l'erreur à partir de l'estimation et des valeurs réelles :

  • erreur = f(estimation, groundtruth)

• mise à jour de l'estimation :

  • estimation = estimation *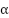* f(erreur)

• stop en fonction d'un seuil d'erreur minimal.

En pratique, étant donné un jeu de données, cela donne :

Phase d'initialisation du vecteur h, par exemple uniquement des zéros.

À chaque itération, tant que l'erreur est assez grosse :

• sélection les échantillons (aléatoire ou sous-échantillonnage) ;

• calcul de l'erreur d'estimation en fonction de h: e = f(h) ;

• màj de h en fonction de l'erreur: h = h + 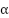* e .

En pratique, le paramètre sert à régler la rapidité de convergence de l'algorithme et la précision des résultats.

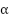• petit : convergence lente mais meilleure précision ;

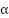• grand : convergence rapide mais résultat moins précis ;

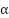• trop grand : explosion et non convergence.

Le learning rate est un des paramètres principaux des modèles que vous serez amené à entraîner.

En résumé

• Il y a en pratique 3 types de modèles couramment utilisés : linéaire, à base d'arbres et réseaux de neurones. 

• Il faut distinguer le type du modèle (c’est-à-dire sa classe, sa famille), de sa version instanciée, qui est entraînée sur un jeu de données et prête à faire des prédictions. 

• Un algorithme est la répétition d'un calcul simple qui permet d'approcher de façon itérative le résultat attendu. 

• L'erreur d'estimation est un élément clé de l'algorithme et du modèle de ML qui permet de juger de la pertinence de l'estimation.

Le Machine Learning est composé de variantes et de méthodes diverses dont nous allons voir quelques exemples.