Initiez-vous au Machine Learning

Pour finir ce cours nous allons travailler sur l'apprentissage d'ensemble ou ensemble learning.

En somme, au lieu de prendre l'avis d'un expert (rôle jusqu'ici joué par un modèle optimisé), nous nous fions au vote de nombreux amateurs (rôle joué par les modèles peu performants). C'est du Machine Learning profondément démocratique ! La sagesse des foules appliquée au Machine Learning.

Dans la pratique, l'apprentissage d'ensemble permet de réduire le biais et l'overfit d'un modèle et de lui apporter robustesse et stabilité face aux outliers et au bruit.

On considère 2 techniques :

1. Le bagging qui, appliqué aux arbres de décision, donne naissance au modèle de forêt aléatoire.

2. Le boosting qui engendre la famille des XGBoost. Plus délicat à optimiser que les forêts aléatoires, XGBoost est souvent le modèle gagnant sur des données tabulaires.

Découvrez le principe du bagging et des forêts aléatoires

Le bagging consiste à entraîner de multiples instances d'un modèle dont les performances sont par construction faibles. On appelle ce modèle de base un weak learner (ou prédicteur faible). Par exemple : un arbre de décision fortement contraint en profondeur.

On entraîne de nombreuses instances de ces prédicteurs faibles. Chaque instance est entraînée sur une partie des données d'entraînement et sur une partie des variables prédictives.

On combine ensuite les prédictions des prédicteurs faibles pour former le modèle d'ensemble.

• Pour la régression : la moyenne des prédictions des prédicteurs faibles.

• Pour la classification : le vote. La catégorie prédite par l'ensemble correspond à la catégorie la plus souvent prédite par les prédicteurs faibles.

On retrouve dans ces 2 modèles les paramètres d'un arbre de décision, (tels que   max_depth  …) auxquels s'ajoutent les paramètres spécifiques à l'apprentissage d'ensemble :

• n_estimators  : le nombre d'arbres dans la forêt ;

• max_features  : le nombre de variables considérées pour chaque arbre ;

• bootstrap  : indique si chaque arbre est entraîné sur l'intégralité du jeu de données ou une partie échantillonnée.

Chargez le dataset “Hastie”

Dans ce chapitre nous allons utiliser un dataset artificiel appelé Hastie, issu du livre Elements of Statistical Learning de Hastie, Tibshirani et Friedman, la référence en Machine Learning. Il est plus adapté pour faire des démonstrations sur les random forests et le XGBoost que ne l'est notre dataset d'arbres.

from  sklearn.datasets import make_hastie_10_2
X, y = make_hastie_10_2(n_samples=12000, random_state=808)

Réduisez le biais

Regardons comment évolue le score de notre classification du stade de développement en accroissant le nombre d'arbres. On considère un arbre de profondeur 2 comme modèle de base. Le nombre d'arbres dans la forêt varie de 1 à 120.

tree_counts = [1,2,3,4,5,10,15,20,25,30,40,50, 60, 70, 80, 90, 100, 110, 120]
X_train, X_test, y_train, y_test = train_test_split( X, y, train_size=0.8, random_state=8)

accuracy  = []
for n_estimator in tree_counts:
    clf = RandomForestClassifier(
        n_estimators = n_estimator,
        max_depth = 2,
        random_state = 8
        )

    clf.fit(X_train, y_train)
    accuracy.append(clf.score(X_test, y_test))

La fonction score du  RandomForestClassifier  donne l'accuracy :

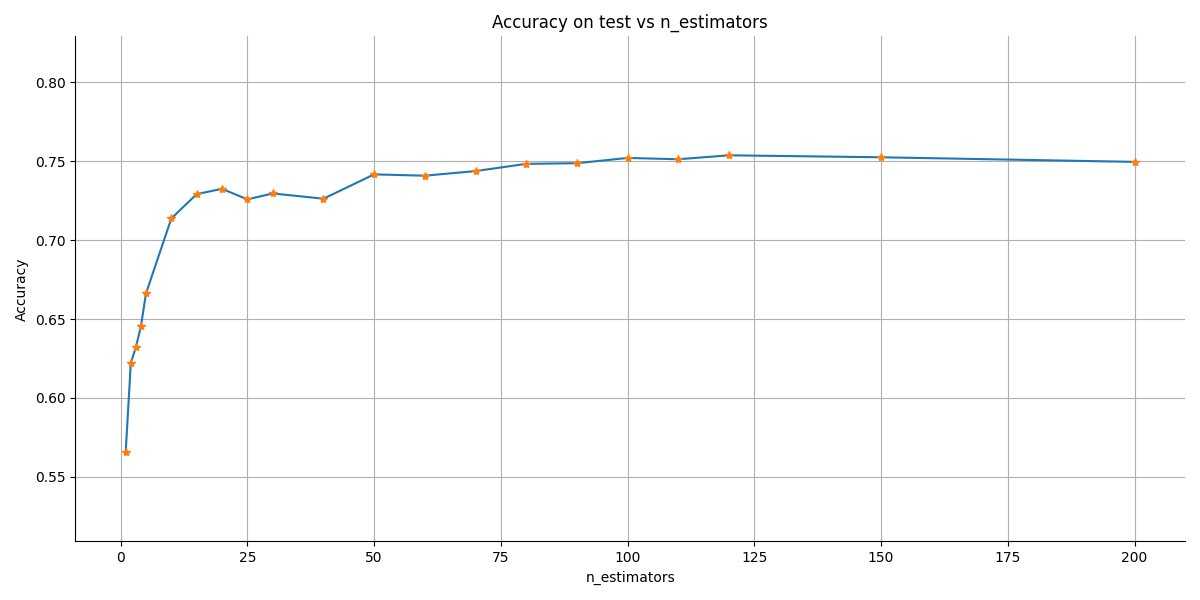
Le score atteint un plateau à partir de 50 arbres.

Réduisez la variance

Le bagging permet aussi de réduire l'overfit d'un modèle. Prenons comme modèle de base un arbre dont la profondeur n'est pas contrainte et qui, par conséquent, overfit. Fixons aussi le paramètre  max_features  de façon à ce que toutes les variables soient prises en compte dans chaque prédicteur faible.

        clf = RandomForestClassifier(
            n_estimators = n_estimator,
            max_depth = None,
            max_features = None,
            random_state = 8
            )

Regardons maintenant l'évolution des scores en fonction du nombre d'arbres dans la forêt aléatoire :

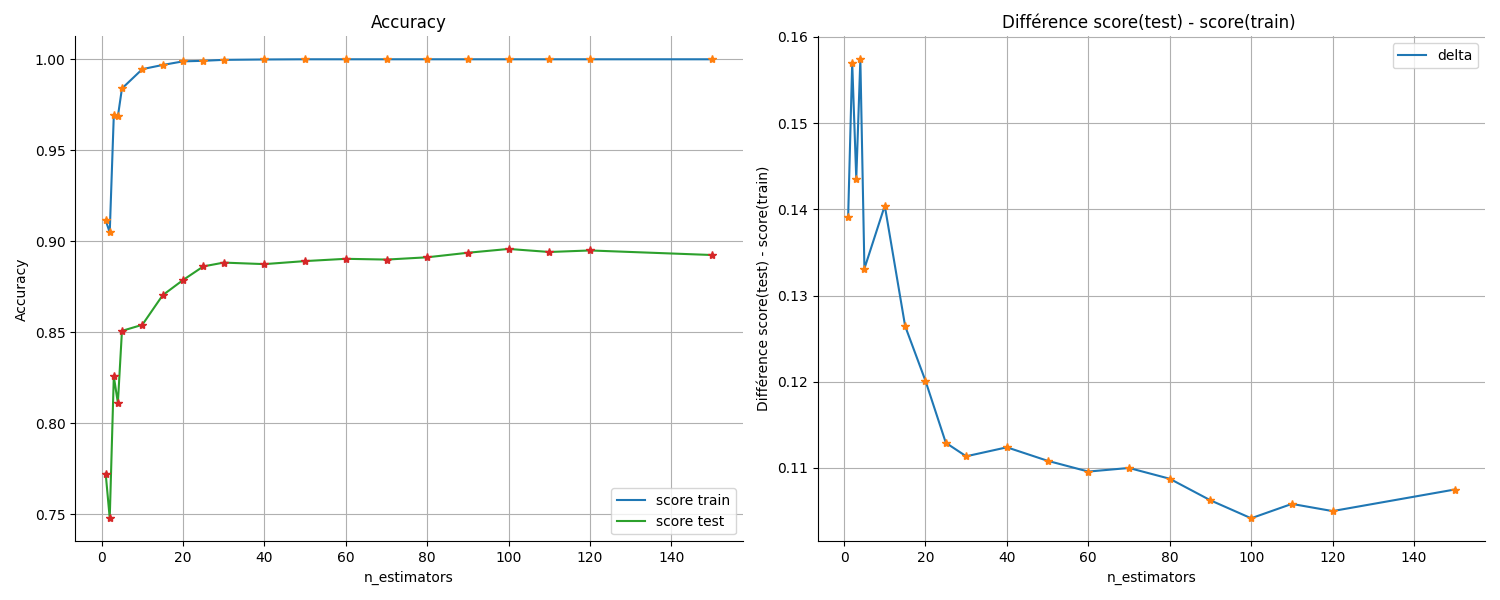
À gauche, le score sur les sous-ensembles d'entraînement et de test et à droite leur différence.

Le modèle a rapidement un score excellent, même parfait à 1, sur le sous-ensemble d'entraînement, mais au fur et à mesure que l'on rajoute des arbres, le score d'extrapolation sur les données de test continue de croître.

De même l'écart entre les 2 scores (test et train) diminue sensiblement alors que l'on rajoute des estimateurs dans la forêt aléatoire.

Donc la forêt aléatoire est un modèle fantastique pour réduire l'overfit de multiples façons :

• augmenter le nombre d'arbres ;

• contraindre l'arbre de base en réduisant  max_depth  ;

• réduire le nombre de variables sur lesquelles chaque arbre de base est entraîné.

Estimez l’importance de chaque variable

Comme chaque arbre n'est pas entraîné sur toutes les variables, il est possible d'estimer l'importance de chaque variable.

Reprenons notre dataset sur les arbres en version numérisée :

filename = <...>

data = pd.read_csv(filename)
X = data[['domanialite', 'arrondissement','libelle_francais', 'genre', 'espece','circonference_cm', 'hauteur_m']]
y = data.stade_de_developpement.values

X_train, X_test, y_train, y_test = train_test_split( X, y, train_size=0.8, random_state=808)

et entraînons une forêt aléatoire :

clf = RandomForestClassifier(
    n_estimators = 100,
    random_state = 8
    )

clf.fit(X_train, y_train)

print(clf.feature_importances_)
[0.039, 0.161 0.041 0.037 0.056 0.462 0.205]

En ordonnant les variables en fonction de leur importance relative, on obtient la figure :

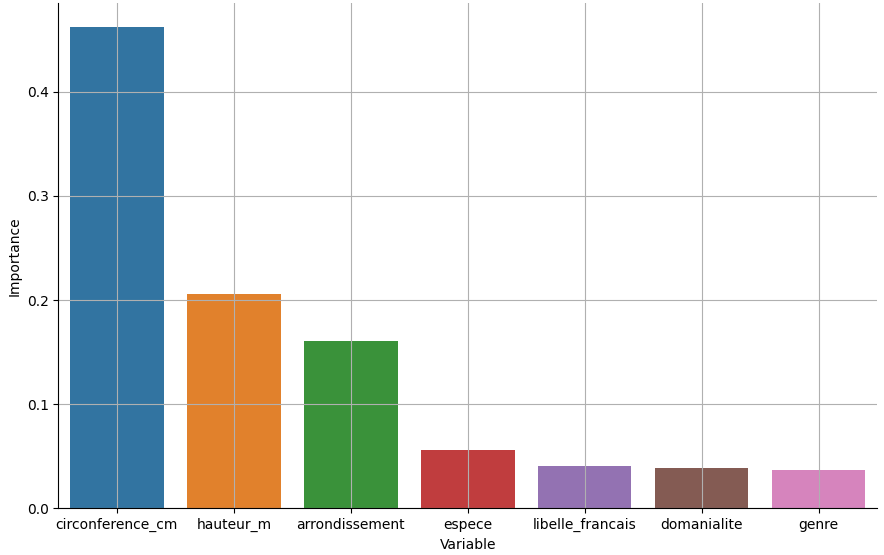
La variable principale est la circonférence suivie par la largeur. L'arrondissement est aussi important.

Découvrez le principe du boosting appliqué aux arbres de décision

Toutes ces librairies implémentent des versions légèrement différentes de XGBoost et se distinguent par :

• leur rapidité d'entraînement ;

• l'optimisation de la mémoire de l'ordinateur ;

• la constitution des ensembles d'arbres ;

• le traitement des variables catégoriques ;

• le nom et la signification des paramètres.

Il nous faut prendre en compte un nouveau paramètre qui provient de la partie gradient du  GradientBoosting  : le  learning_rate  ou taux d'apprentissage qui dicte la quantité de corrections prises en compte à chaque itération.

Sélectionnez les paramètres d'un Gradient Boosting

Optimiser un modèle devient plus difficile au fur et à mesure que le nombre de paramètres augmente. Aux paramètres des arbres de décision et à ceux des forêts aléatoires s'ajoutent maintenant ceux de la partie gradient stochastique du  GradientBoosting  , entre autres le  learning_rate  .

Une bonne stratégie consiste à optimiser en premier lieu le nombre d'arbres :

1. Fixez   max_depth  à  3  , et le learning-rate à  0.1  .

2. Optimisez le nombre d'arbres en faisant un  grid search  avec validation croisée sur différentes valeurs. Par exemple : 10, 50, 100, 200, 500.

3. Une fois le nombre d'arbres optimal trouvé, optimisez le  learning rate  . Pour optimiser le  learning rate  , gardez en tête que :

• un  learning rate  élevé fait converger l'algorithme rapidement au détriment de l'erreur ;

• en réduisant le  learning rate  , vous allez ralentir la convergence de l'algorithme mais en même temps réduire l'erreur jusqu'à atteindre un plateau.

Faites varier ensuite le  max-depth  mais à ce stade cela ne devrait pas changer grand-chose.

Tout cela dépend évidemment énormément de votre contexte.

Réduisez la variance

Les forêts aléatoires overfittent rarement. Par contre, les "boosted trees" peuvent plus facilement overfitter. Mais on peut maintenant aussi jouer sur la valeur du learning rate.

Reprenons le dataset de Hastie et comparons la performance du modèle en fonction des valeurs décroissantes du  learning rate  . Cette fois-ci on regarde le score sur le sous-ensemble de test au fur et à mesure des itérations du modèle.

On utilise une nouvelle métrique pour la classification. Le  log_loss  qui prend en compte l'écart entre la probabilité de la prédiction d'appartenir à la bonne classe et la classe réelle. Par exemple un échantillon qui a un score de proba de  0.6  et qui donc appartient a la catégorie 1 sera pénalisé par rapport à un échantillon avec un score de  0.9  .

On peut obtenir la probabilité des prédictions du modèle à chaque itération grâce à la fonction  staged_predict_proba  :

from sklearn.ensemble import GradientBoostingClassifier

learning_rates = [1, 0.6,  0.3, 0.1]
for lr in learning_rates:

    clf = GradientBoostingClassifier(
          n_estimators= 500,
          max_depth= 2,
          random_state= 8,
          learning_rate= lr
    )
    clf.fit(X_train, y_train)

Voici le code pour calculer le  log_loss  à chaque itération et pour chaque valeur du learning rate :

scores = np.zeros((clf.n_estimators,), dtype=np.float64)
for i, y_proba in enumerate(clf.staged_predict_proba(X_test)):
  scores[i] =  log_loss(y_test, y_proba[:, 1])

On obtient la figure suivante :

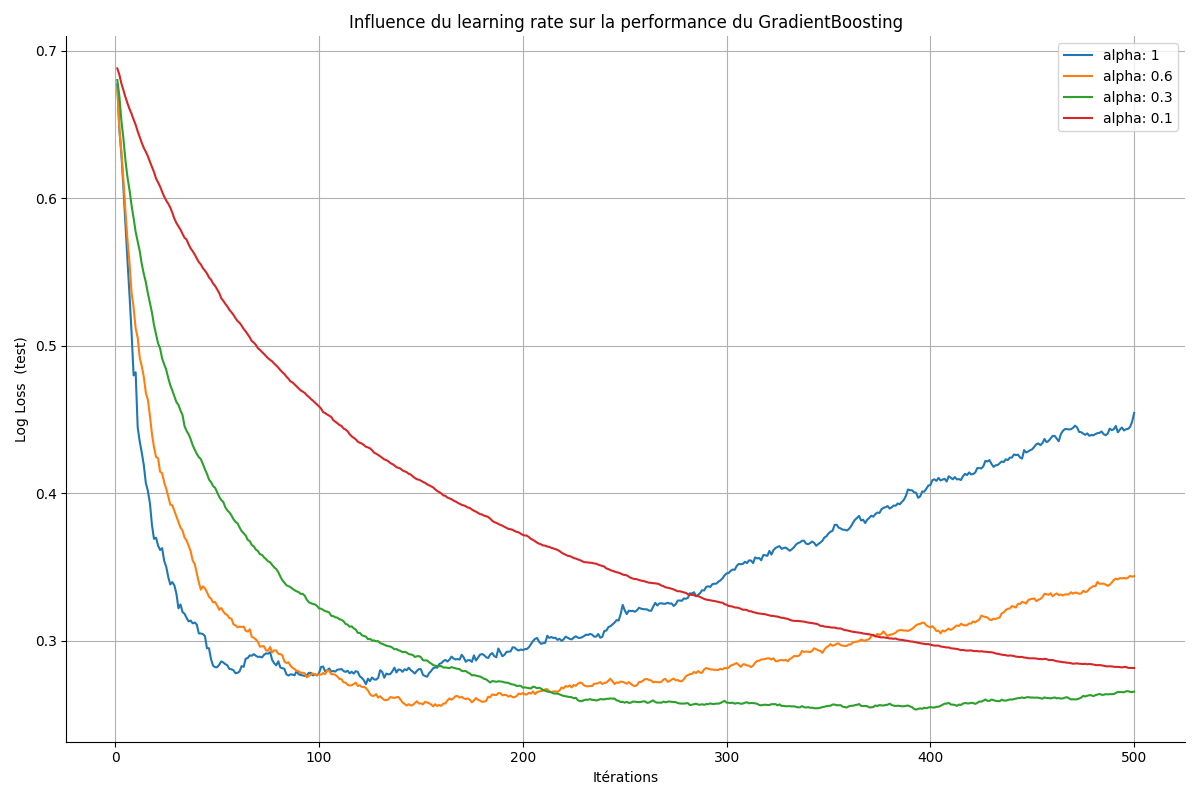
On observe que :

• learning_rate = 1  ou  0.6  , le modèle converge puis diverge. Le score sur le test repart à la hausse après avoir diminué. Le modèle perd sa capacité d'extrapolation.

• Pour  learning_rate = 0.1  , le modèle converge mais plus lentement que pour  learning_rate = 0.3  .

C'est là une illustration rapide du type de comportement auquel vous pouvez vous attendre en réglant le  learning rate  du Gradient Boosting.

Choisissez le bon modèle parmi tous les modèles de scikit-learn

Pour finir, un mot sur le choix du modèle lorsque l'on débute sur un nouveau problème et un nouveau dataset. Avec scikit-learn vous avez l'embarras du choix, et il peut sembler difficile de sélectionner le bon modèle.

Une stratégie simple consiste à commencer par une régression linéaire / logistique pour comprendre les dynamiques entre les variables de prédiction et la variable cible. Cela vous permettra de sélectionner les meilleures variables prédictives et d'obtenir un benchmark des performances attendues.

La régression linéaire ou logistique est parfaite pour fixer ce benchmark car le modèle est simple et les scores obtenus très probablement améliorables avec des modèles plus complexes. Une fois ce benchmark établi, optimisez une forêt aléatoire. Vous devriez obtenir de bien meilleurs scores qu'avec une simple régression.

Selon les contextes, les forêts aléatoires sont parfois plus efficaces que les modèles GradientBoosting. Mais si les scores obtenus ne donnent pas satisfaction, il sera temps d'entraîner un XGBoost.

En résumé

• L'apprentissage d'ensemble donne naissance à des modèles robustes et performants moins sujets au sur-apprentissage.

• Les forêts aléatoires consistent à entraîner de multiples arbres de décision en parallèle et à moyenner leurs prédictions. Contraindre la profondeur des arbres correspond à une régularisation qui compense le sur-apprentissage.

• Le Gradient Boosting enchaîne l'entraînement d'arbres de décision en se concentrant sur les erreurs de la séquence. C'est en général le modèle qui  sera le plus efficace, mais il est plus délicat à paramétrer. 

• Définir un benchmark avec une simple régression pour fixer les attentes en termes de performance est une bonne pratique avant de se lancer dans l'entraînement de modèles ensemblistes.

Bravo d'avoir suivi le cours jusque-là. J'espère qu'il vous a intéressé et surtout qu'il vous a donné les éléments pour continuer à découvrir ce domaine incroyable qu'est le Machine Learning. Nous avons couvert beaucoup de sujets, de jeux de données et de modèles mais j'ai dû en laisser de côté.

Si vous souhaitez continuer à approfondir le domaine, je ne peux que vous conseiller de regarder de plus près le gradient stochastique, indémodable et central à de nombreux modèles et techniques, dont le Deep Learning. Mais aussi de vous frotter au Machine Learning dans le cloud et notamment aux outils d'AutoML tels que Vertex AI de Google, qui sont d'une efficacité redoutable.

Il vous reste un dernier quiz pour tester votre compréhension des concepts de la dernière partie du cours ! Sur ce, je vous souhaite une belle continuation et de bonnes explorations !