Analysez et modélisez des séries temporelles

On souhaite désaisonnaliser la série temporelle airpass à l'aide de la régression linéaire.

On créé à cet effet les bases tendancielle et saisonnière :

t=1:144

for (i in 1:12)
{
  su=rep(0,times=12)
  su[i]=1
  s=rep(su,times=12)
  assign(paste("s",i,sep=""),s)
}

On effectue la régression linéaire (le modèle est transformé, comme vu en cours, afin de pallier le problème de colinéarité) sur la série $\$\backslash (Y\_t\backslash )\$$  :

reg=lm(y~t+s1+s2+s3+s4+s5+s6+s7+s8+s9+s10+s11+s12-1)
summary(reg)

On obtient l'estimation des différents paramètres :

## 
## Call:
## lm(formula = y ~ t + s1 + s2 + s3 + s4 + s5 + s6 + s7 + s8 + 
## s9 + s10 + s11 + s12 - 1)
## 
## Residuals:
## Min 1Q Median 3Q Max 
## -0.156370 -0.041016 0.003677 0.044069 0.132324 
## 
## Coefficients:
## Estimate Std. Error t value Pr(>|t|) 
## t 0.0100688 0.0001193 84.4 <2e-16 ***
## s1 4.7267804 0.0188935 250.2 <2e-16 ***
## s2 4.7047255 0.0189443 248.3 <2e-16 ***
## s3 4.8349527 0.0189957 254.5 <2e-16 ***
## s4 4.8036838 0.0190477 252.2 <2e-16 ***
## s5 4.8013112 0.0191003 251.4 <2e-16 ***
## s6 4.9234574 0.0191535 257.1 <2e-16 ***
## s7 5.0273997 0.0192073 261.7 <2e-16 ***
## s8 5.0181049 0.0192617 260.5 <2e-16 ***
## s9 4.8734703 0.0193167 252.3 <2e-16 ***
## s10 4.7353120 0.0193722 244.4 <2e-16 ***
## s11 4.5915943 0.0194283 236.3 <2e-16 ***
## s12 4.7054593 0.0194850 241.5 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0593 on 131 degrees of freedom
## Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999 
## F-statistic: 9.734e+04 on 13 and 131 DF, p-value: < 2.2e-16

Les différents coefficients sont contenues dans `reg$coefficients` :

reg$coefficients

## t s1 s2 s3 s4 s5 s6 
## 0.0100688 4.7267804 4.7047255 4.8349527 4.8036838 4.8013112 4.9234574 
## s7 s8 s9 s10 s11 s12 
## 5.0273997 5.0181049 4.8734703 4.7353120 4.5915943 4.7054593

On revient aux coefficients initiaux :

a=mean(reg$coefficients[2:13])
b=reg$coefficients[1]
c=reg$coefficients[2:13]-mean(reg$coefficients[2:13])

et on obtient la série corrigée des variations saisonnières (en n'oubliant pas de passer à l'exponentiel pour revenir à $\$\backslash (X\_t\backslash )\$$ ) :

y_cvs=y-(c[1]*s1+c[2]*s2+c[3]*s3+c[4]*s4+c[5]*s5+c[6]*s6+c[7]*s7+c[8]*s8+c[9]*s9+c[10]*s10+c[11]*s11+c[12]*s12)
x_cvs=exp(y_cvs)
ts.plot(x,x_cvs,xlab="t",ylab="Airpass",col=c(1,2),lwd=c(1,2))
legend("topleft",legend=c("X","X_CVS"),col=c(1,2),lwd=c(1,2))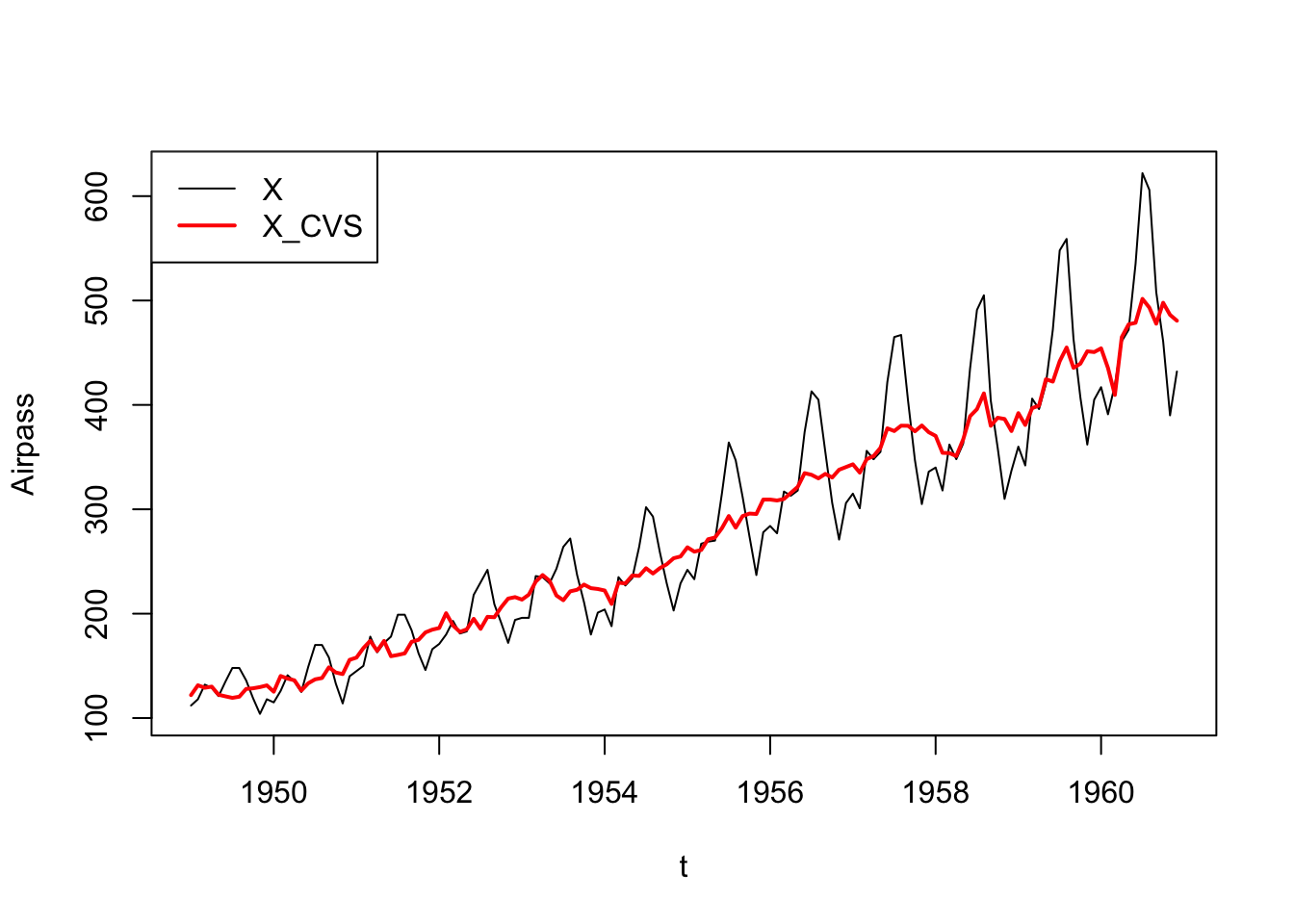

On constate que la série CVS présente des baisses en 1958 et 1960, pas forcément perceptibles à l'oeil nu sur la série brute. On pourra vérifier que la méthode des moyennes mobiles mettra en évidence les mêmes ruptures.