Stationnarisation de la série
On désigne par la série airpass, et on considère . On travaille en effet sur le logarithme de la série afin de pallier l’accroissement de la saisonnalité. On passe ainsi d’un modèle multiplicatif à un modèle additif.
plot(acf(y,lag.max=36,plot=FALSE),ylim=c(-1,1)) 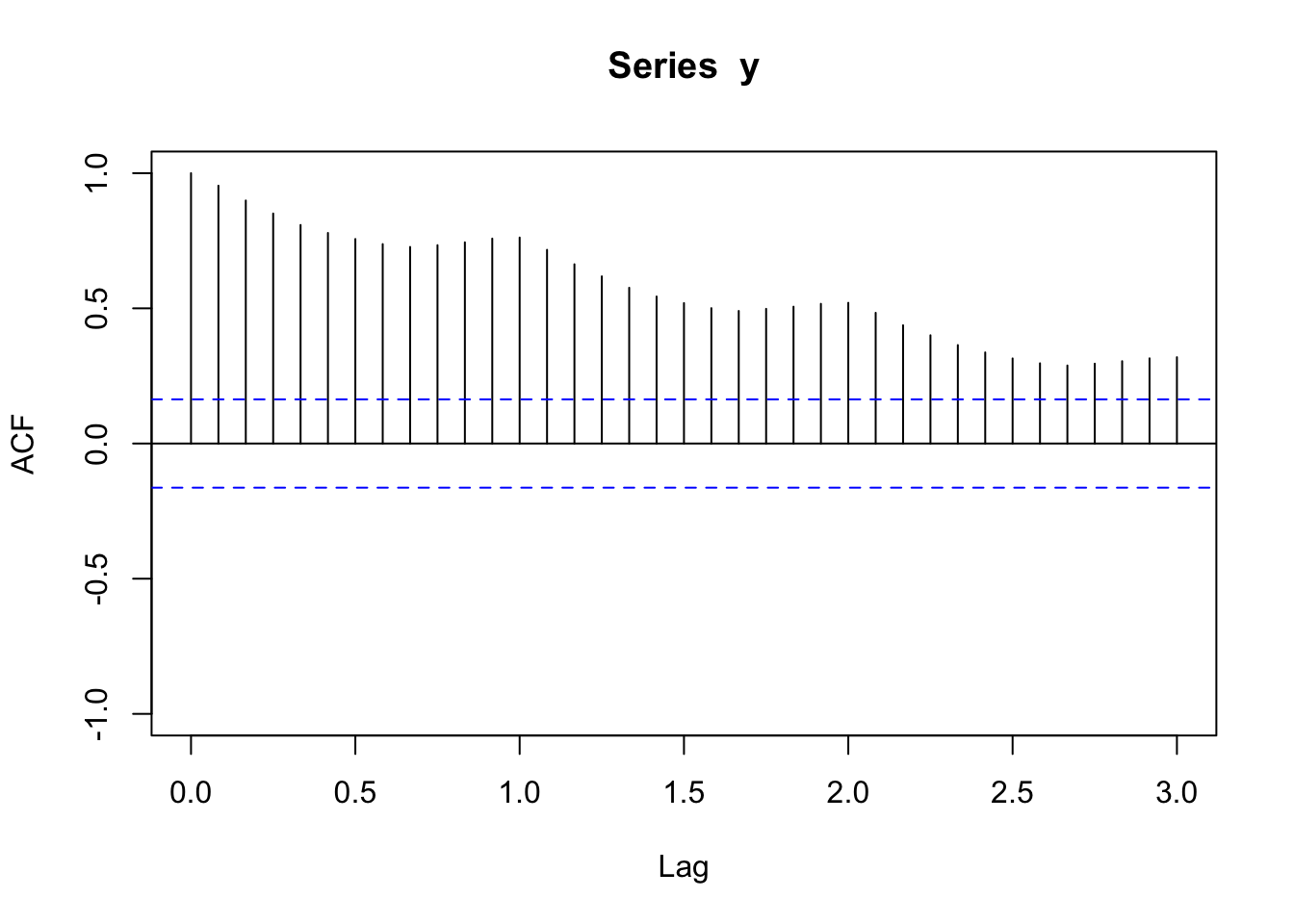
La sortie ACF présente une décroissance lente vers 0, ce qui traduit un problème de non-stationnarité. On effectue donc une différenciation .
y_dif1=diff(y,lag=1,differences=1)
plot(acf(y_dif1,lag.max=36,plot=FALSE),ylim=c(-1,1))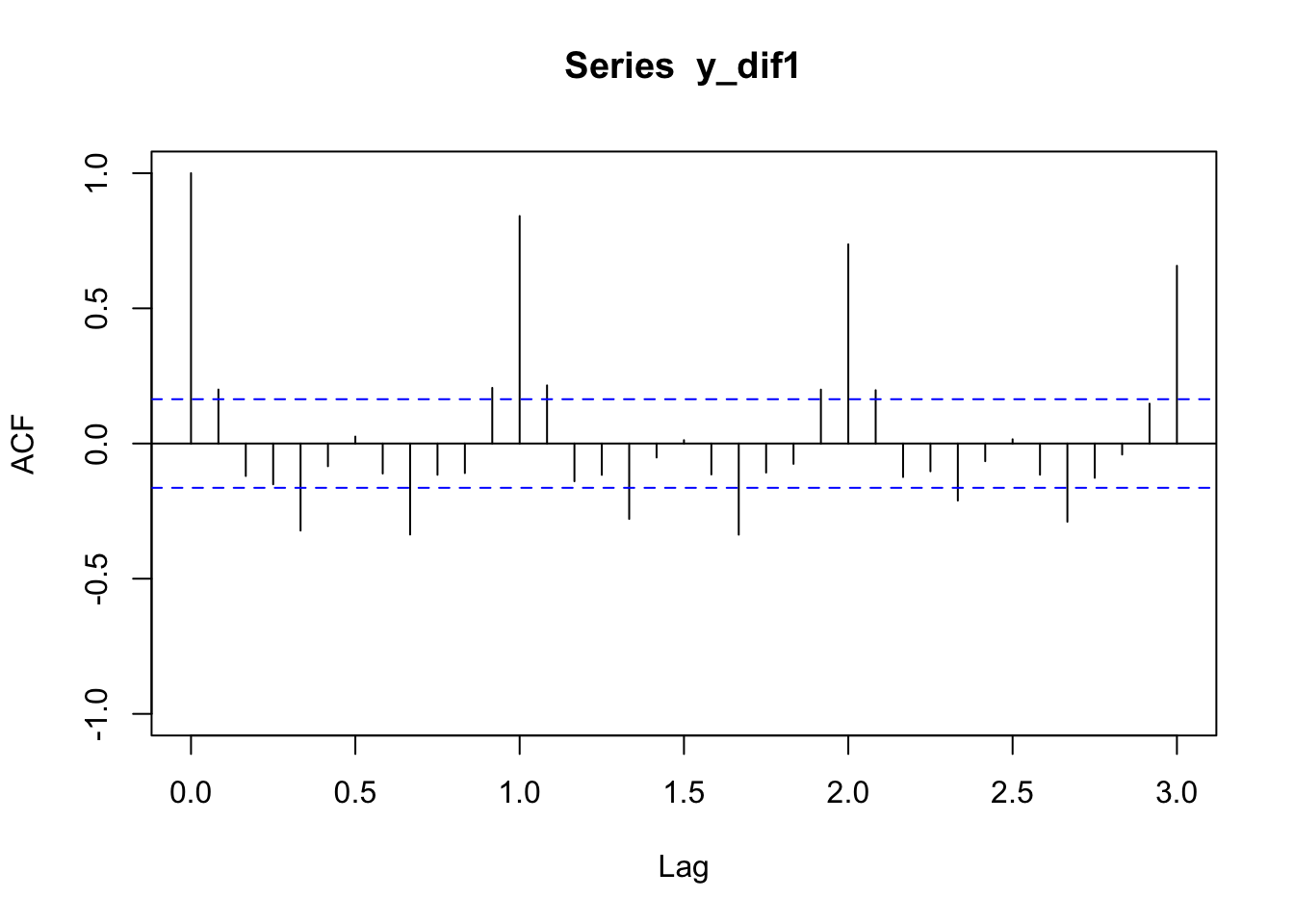 La sortie ACF de la série ainsi différenciée présente encore une décroissance lente vers 0 pour les multiples de 12. On effectue cette fois la différenciation .
La sortie ACF de la série ainsi différenciée présente encore une décroissance lente vers 0 pour les multiples de 12. On effectue cette fois la différenciation .
y_dif_1_12=diff(y_dif1,lag=12,differences=1)
plot(acf(y_dif_1_12,lag.max=36,plot=FALSE),ylim=c(-1,1))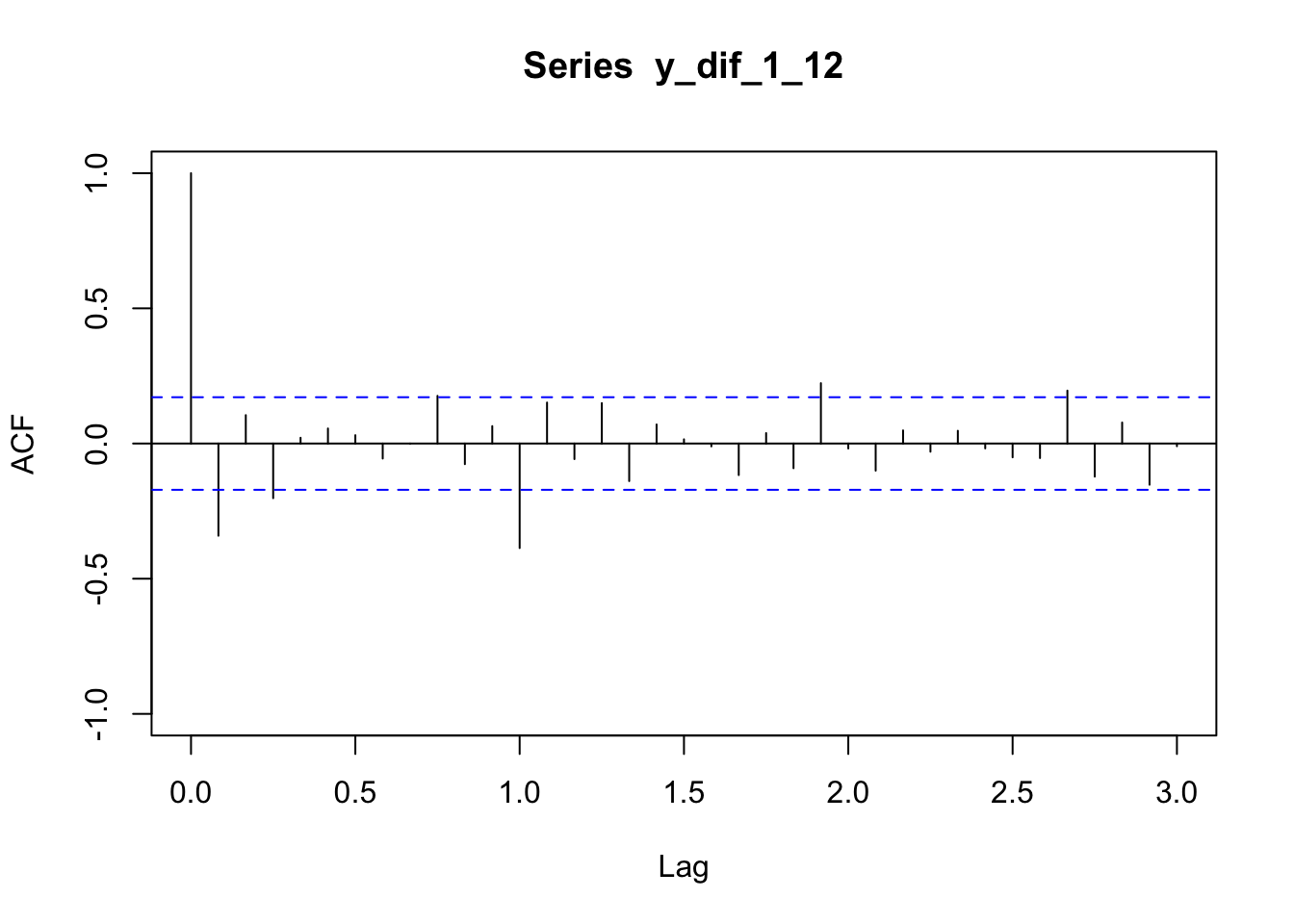
La sortiE ACF de la série doublement différenciée semble pouvoir être interprétée comme un autocorrélogramme simple empirique. On identifiera donc un modèle ARMA sur la série
Identification, estimation et validation de modèles
On s’appuie sur les autocorrélogrammes simple et partiels estimés :
y_dif_1_12=diff(y_dif1,lag=12,differences=1)
plot(acf(y_dif_1_12,lag.max=36,plot=FALSE),ylim=c(-1,1))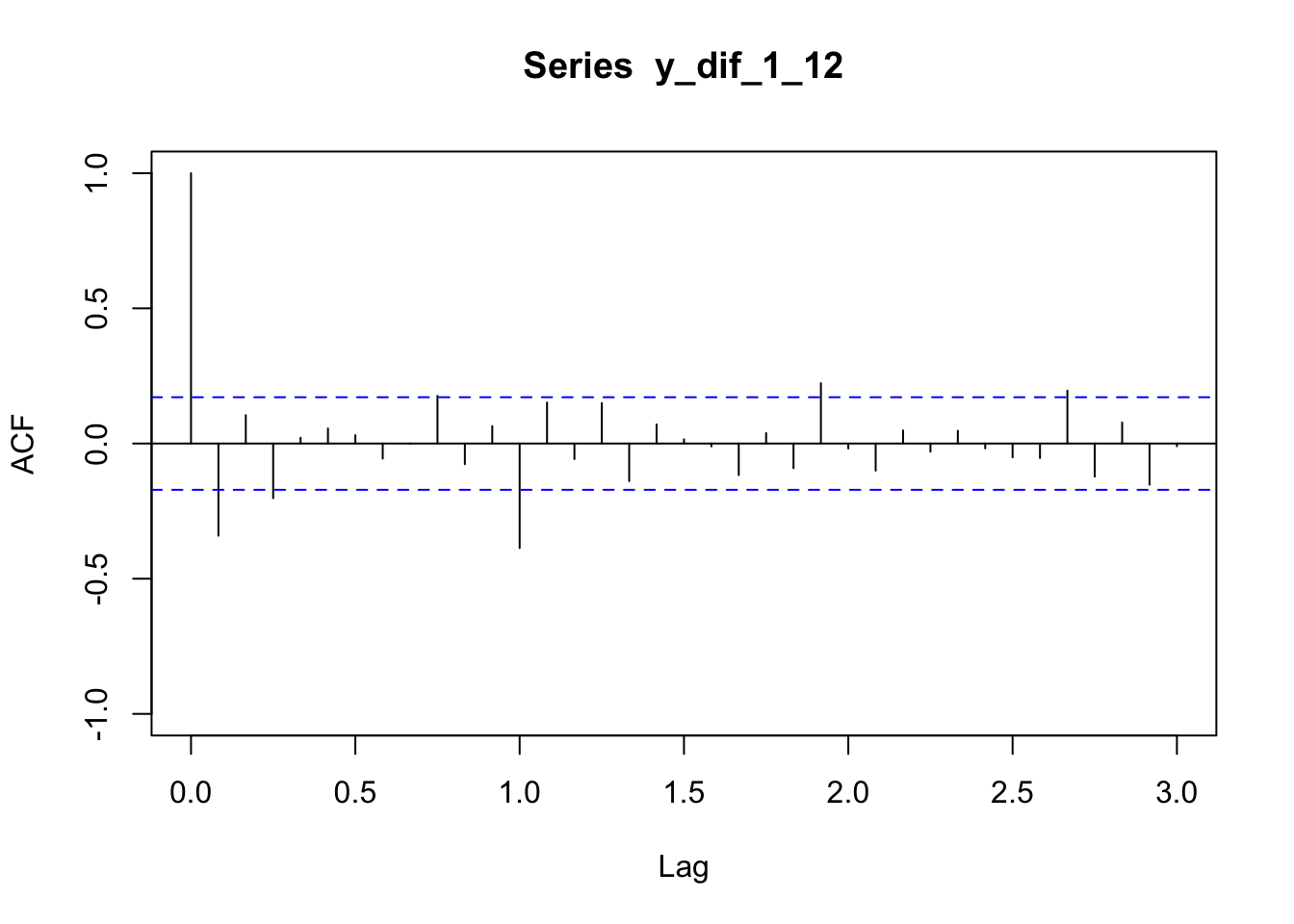
plot(pacf(y_dif_1_12,lag.max=36,plot=FALSE),ylim=c(-1,1))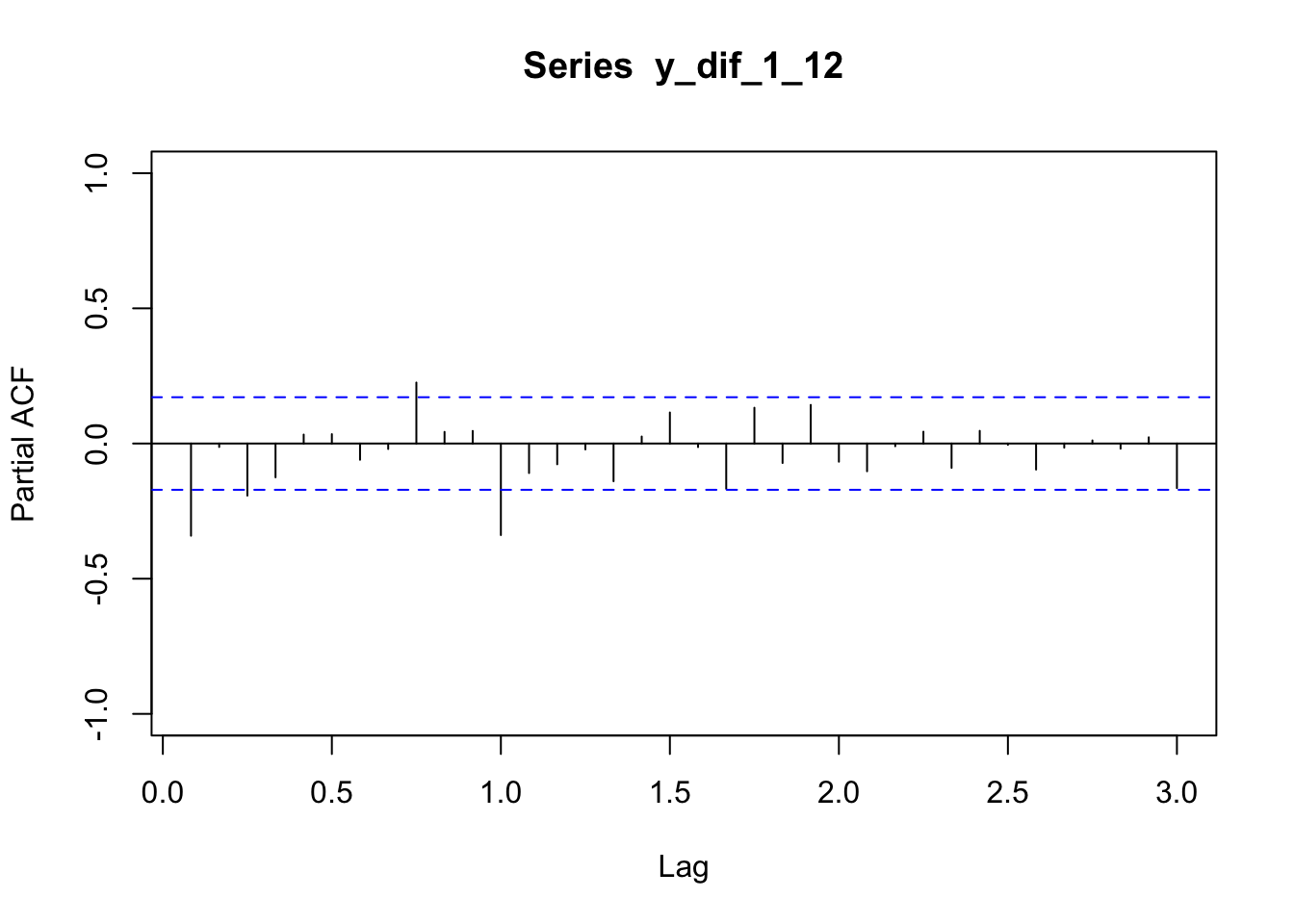
Modèle 1
On estime en premier lieu un modèle au vu des autocorrélogrammes empiriques simples et partiels. Ce modèle s’écrit :
model1=Arima(y,order=c(1,1,1),list(order=c(1,1,1),period=12),include.mean=FALSE,method="CSS-ML")
summary(model1)
## Series: y
## ARIMA(1,1,1)(1,1,1)[12]
##
## Coefficients:
## ar1 ma1 sar1 sma1
## 0.1666 -0.5615 -0.099 -0.4973
## s.e. 0.2459 0.2115 0.154 0.1360
##
## sigma^2 estimated as 0.00138: log likelihood=245.16
## AIC=-480.31 AICc=-479.83 BIC=-465.93
##
## Training set error measures:
## ME RMSE MAE MPE MAPE
## Training set 0.0006239395 0.03489259 0.02595463 0.01199887 0.4696646
## MASE ACF1
## Training set 0.2144266 -0.01250397
t_stat(model1)
## ar1 ma1 sar1 sma1
## t.stat 0.677738 -2.654214 -0.642984 -3.657670
## p.val 0.497938 0.007949 0.520235 0.000255
Box.test.2(model1$residuals,nlag=c(6,12,18,24,30,36),type="Ljung-Box",decim=5)
## Retard p-value
## [1,] 6 0.64051
## [2,] 12 0.81959
## [3,] 18 0.82768
## [4,] 24 0.59646
## [5,] 30 0.75443
## [6,] 36 0.65902Ce modèle ayant des paramètres non significatifs, on en teste un second.
Modèle 2
Soit le modèle :
model2=Arima(y,order=c(1,1,1),list(order=c(0,1,1),period=12),include.mean=FALSE,method="CSS-ML")
summary(model2)
## Series: y
## ARIMA(1,1,1)(0,1,1)[12]
##
## Coefficients:
## ar1 ma1 sma1
## 0.1960 -0.5784 -0.5643
## s.e. 0.2475 0.2132 0.0747
##
## sigma^2 estimated as 0.001375: log likelihood=244.95
## AIC=-481.9 AICc=-481.58 BIC=-470.4
##
## Training set error measures:
## ME RMSE MAE MPE MAPE
## Training set 0.0006214569 0.03495868 0.02587023 0.01205357 0.4682205
## MASE ACF1
## Training set 0.2137293 -0.01530519
t_stat(model2)
## ar1 ma1 sma1
## t.stat 0.792074 -2.712668 -7.554412
## p.val 0.428318 0.006674 0.000000
Box.test.2(model2$residuals,nlag=c(6,12,18,24,30,36),type="Ljung-Box",decim=5)
## Retard p-value
## [1,] 6 0.65243
## [2,] 12 0.80854
## [3,] 18 0.82136
## [4,] 24 0.57705
## [5,] 30 0.74768
## [6,] 36 0.67642Ce modèle ayant des paramètres non significatifs, on en teste un troisième.
Modèle 3
Soit le modèle :
model3=Arima(y,order=c(0,1,1),list(order=c(0,1,1),period=12),include.mean=FALSE,method="CSS-ML")
summary(model3)
## Series: y
## ARIMA(0,1,1)(0,1,1)[12]
##
## Coefficients:
## ma1 sma1
## -0.4018 -0.5569
## s.e. 0.0896 0.0731
##
## sigma^2 estimated as 0.001371: log likelihood=244.7
## AIC=-483.4 AICc=-483.21 BIC=-474.77
##
## Training set error measures:
## ME RMSE MAE MPE MAPE
## Training set 0.0005730622 0.03504883 0.02626034 0.01098898 0.4752815
## MASE ACF1
## Training set 0.2169522 0.01443892
t_stat(model3)
## ma1 sma1
## t.stat -4.482494 -7.618978
## p.val 0.000007 0.000000
Box.test.2(model3$residuals,nlag=c(6,12,18,24,30,36),type="Ljung-Box",decim=5)
## Retard p-value
## [1,] 6 0.51519
## [2,] 12 0.72613
## [3,] 18 0.77822
## [4,] 24 0.50077
## [5,] 30 0.68838
## [6,] 36 0.65352Les tests de significativité des paramètres et de blancheur du résidu sont validés au niveau 5%.
shapiro.test(model3$residuals)
##
## Shapiro-Wilk normality test
##
## data: model3$residuals
## W = 0.98637, p-value = 0.1674Le test de normalité est également validé pour ce modèle.
Prévision à l’aide du modèle retenu (3) de l’année 1961
pred_model3=forecast(model3,h=12,level=95)
pred=exp(pred_model3$mean)
pred_l=ts(exp(pred_model3$lower),start=c(1961,1),frequency=12)
pred_u=ts(exp(pred_model3$upper),start=c(1961,1),frequency=12)
ts.plot(x,pred,pred_l,pred_u,xlab="t",ylab="Airpass",col=c(1,2,3,3),lty=c(1,1,2,2),lwd=c(1,3,2,2))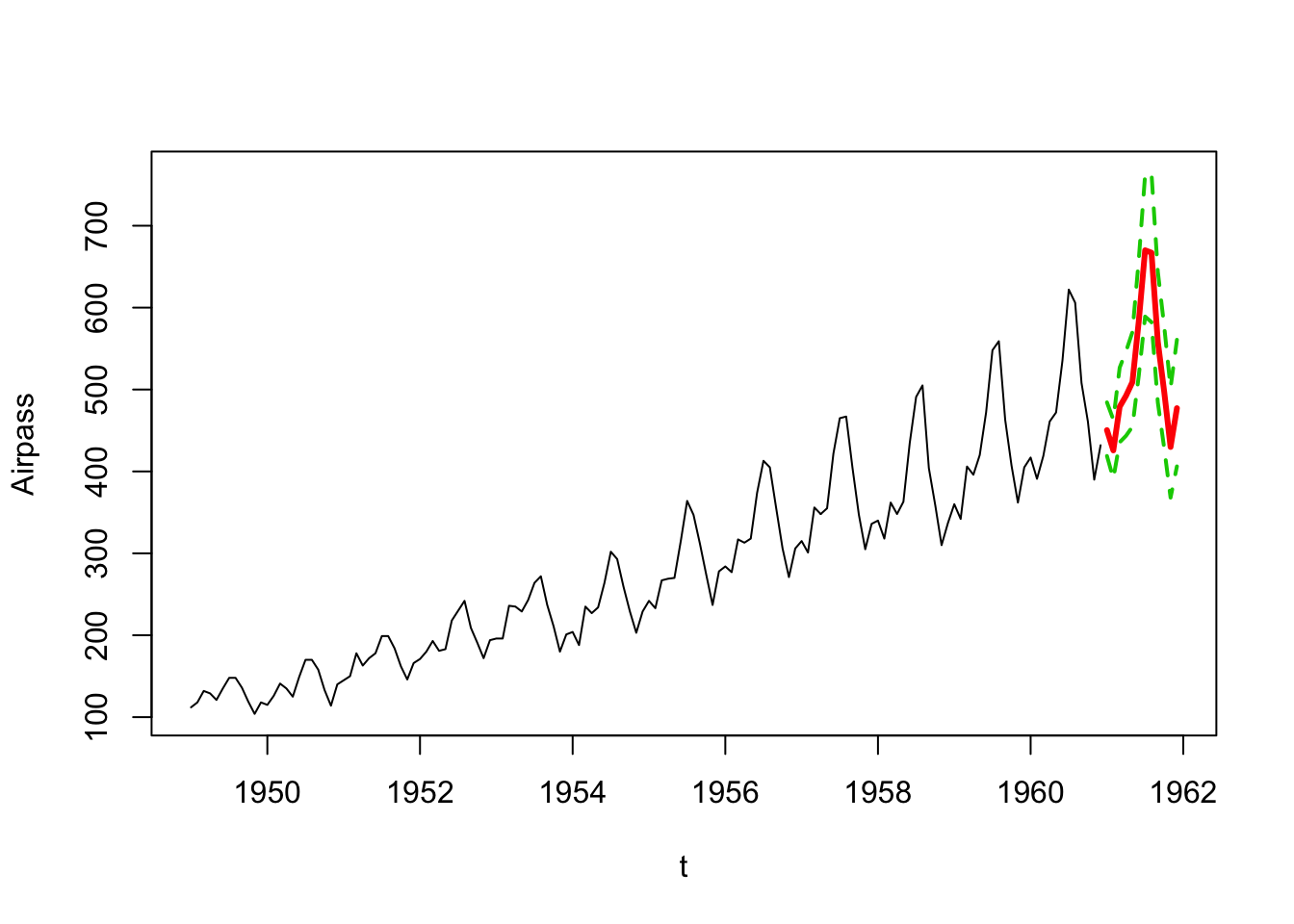
ts.plot(window(x,start=c(1960,1)),pred,pred_l,pred_u,xlab="t",ylab="Airpass",col=c(1,2,3,3),lty=c(1,1,2,2),lwd=c(1,3,2,2))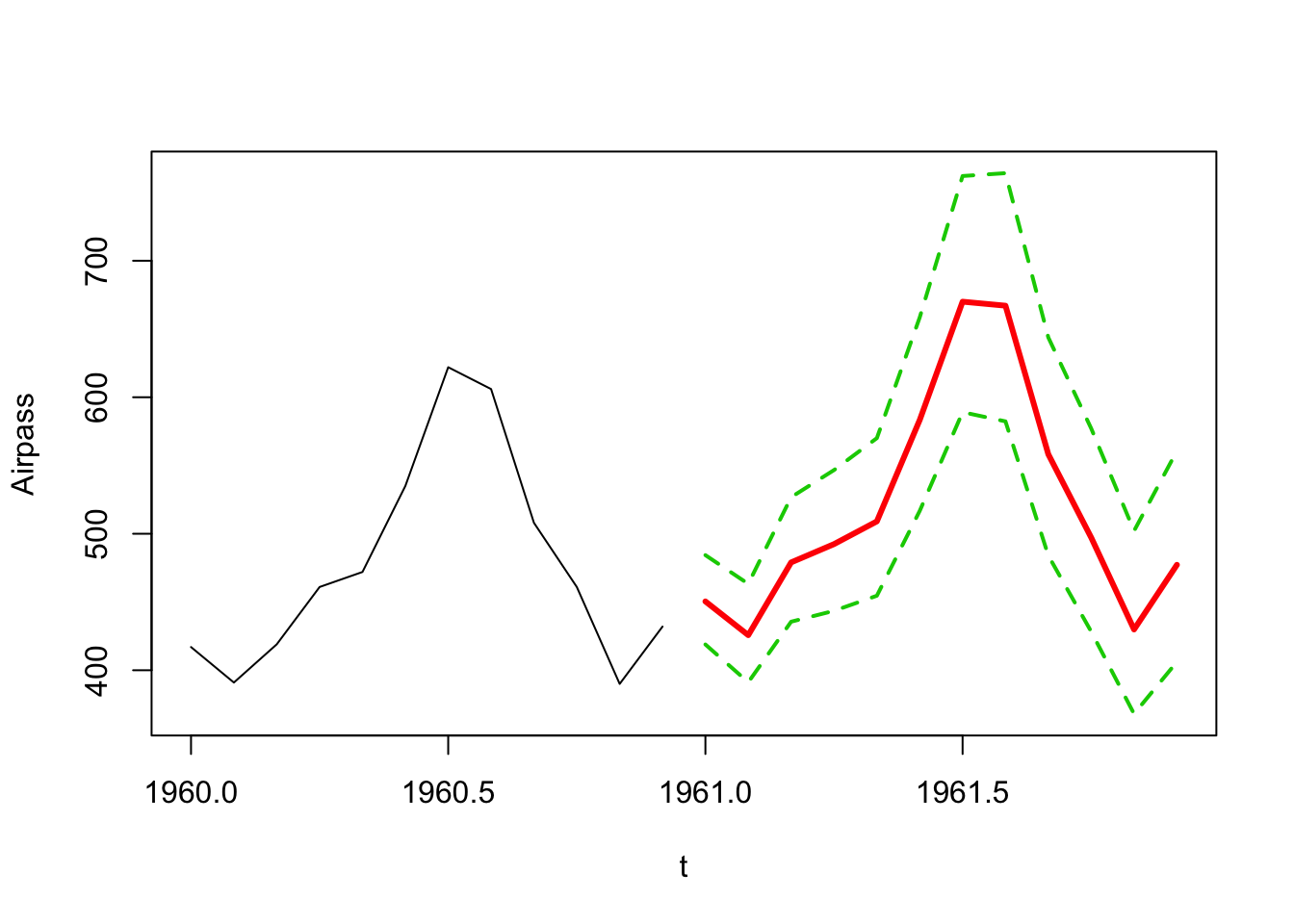
Analyse a posteriori
On tronque la série de l’année 1960, qu’on cherche ensuite à prévoir à partir de l’historique 1949-1959.
x_tronc=window(x,end=c(1959,12))
y_tronc=log(x_tronc)
x_a_prevoir=window(x,start=c(1960,1))On vérifie que le modèle 3 sur la série tronquée est toujours validé.
model3tronc=Arima(y_tronc,order=c(0,1,1),list(order=c(0,1,1),period=12),include.mean=FALSE,method="CSS-ML")
summary(model3tronc)## Series: y_tronc ## ARIMA(0,1,1)(0,1,1)[12] ## ## Coefficients: ## ma1 sma1 ## -0.3484 -0.5623 ## s.e. 0.0943 0.0774 ## ## sigma^2 estimated as 0.001338: log likelihood=223.63 ## AIC=-441.26 AICc=-441.05 BIC=-432.92 ## ## Training set error measures: ## ME RMSE MAE MPE MAPE ## Training set 0.00104934 0.03443221 0.02590904 0.01899277 0.4738142 ## MASE ACF1 ## Training set 0.2113963 0.004637637
t_stat(model3tronc)## ma1 sma1 ## t.stat -3.695894 -7.262873 ## p.val 0.000219 0.000000
Box.test.2(model3tronc$residuals,nlag=c(6,12,18,24,30,36),type="Ljung-Box",decim=5)## Retard p-value ## [1,] 6 0.52539 ## [2,] 12 0.85631 ## [3,] 18 0.87341 ## [4,] 24 0.78327 ## [5,] 30 0.90181 ## [6,] 36 0.84635
shapiro.test(model3tronc$residuals)## ## Shapiro-Wilk normality test ## ## data: model3tronc$residuals ## W = 0.988, p-value = 0.3065
On constate que la réalisation 1960 est dans l’intervalle de prévision à 95% (basé sur les données antérieures à 1959).
pred_model3tronc=forecast(model3tronc,h=12,level=95)
pred_tronc=exp(pred_model3tronc$mean)
pred_l_tronc=ts(exp(pred_model3tronc$lower),start=c(1960,1),frequency=12)
pred_u_tronc=ts(exp(pred_model3tronc$upper),start=c(1960,1),frequency=12)
ts.plot(x_a_prevoir,pred_tronc,pred_l_tronc,pred_u_tronc,xlab="t",ylab="Airpass",col=c(1,2,3,3),lty=c(1,1,2,2),lwd=c(3,3,2,2))
legend("topleft",legend=c("X","X_prev"),col=c(1,2,3,3),lty=c(1,1),lwd=c(3,3))
legend("topright",legend=c("int95%_inf","int95%_sup"),col=c(3,3),lty=c(2,2),lwd=c(2,2))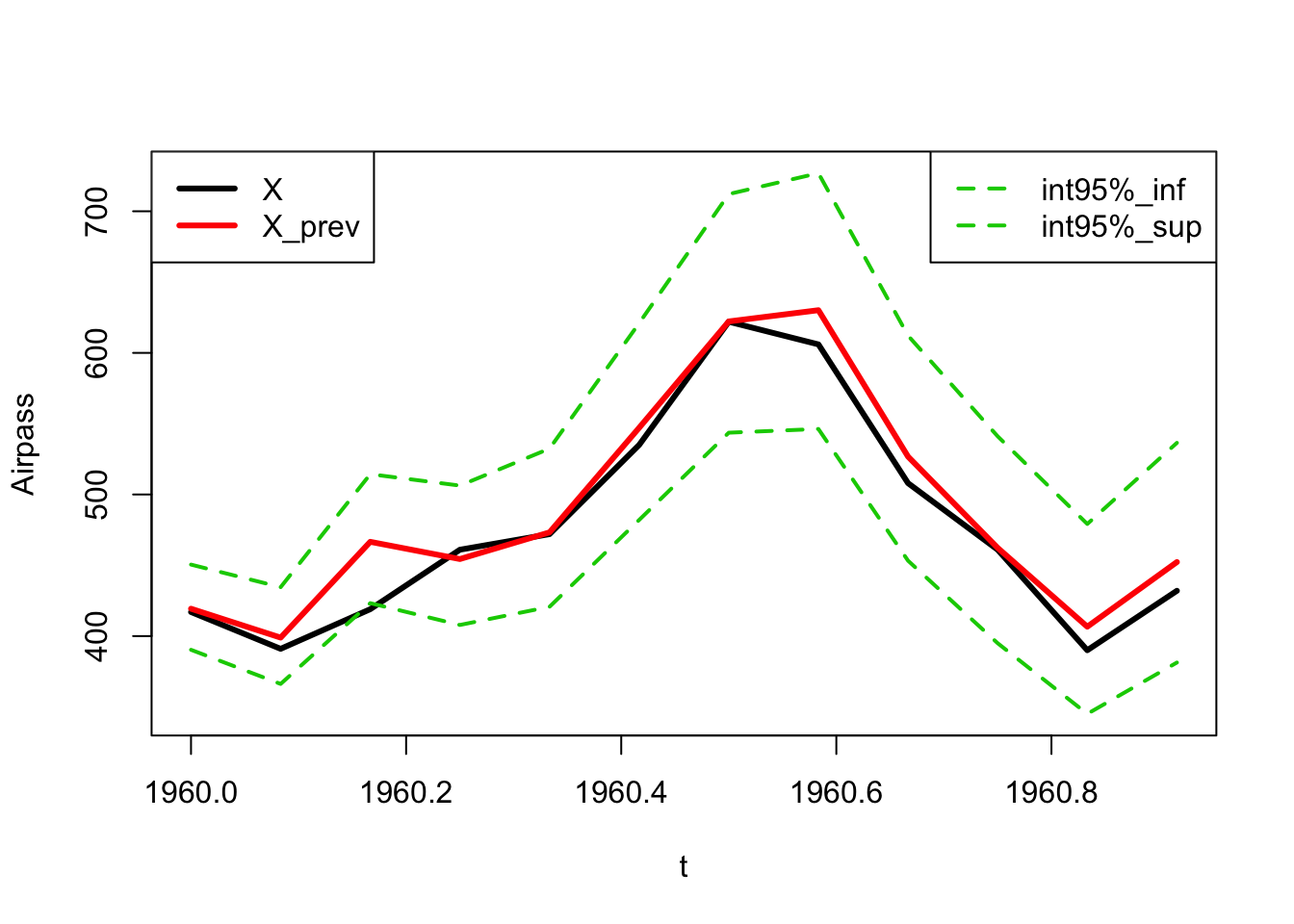
On calcule les RMSE et MAPE.
rmse=sqrt(mean((x_a_prevoir-pred_tronc)^2))
rmse## [1] 18.59359
mape=mean(abs(1-pred_tronc/x_a_prevoir))*100
mape## [1] 2.904473
L’interprétation des critères d’erreur dépend de la série et de la qualité de prévision exigée. Dans le cas présent, un MAPE de 2.9% semble satisfaisant a priori.
