Analysez et modélisez des séries temporelles

Commençons par un algorithme simple

On a comptabilisé pendant trois semaines consécutives le nombre journalier de visiteurs d’un musée dont les jours de fermeture sont le samedi et le dimanche.

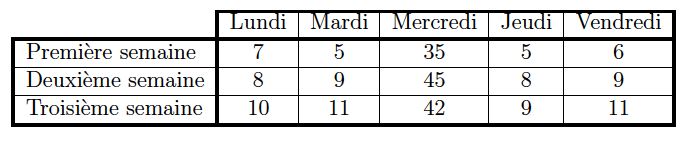
Ces données sont encore représentées dans le tableau ci-dessous (avec en sus la série lissée par moyenne mobile).

Le graphe semble mettre en évidence une tendance linéaire ainsi qu’une saisonnalité de période 5 :

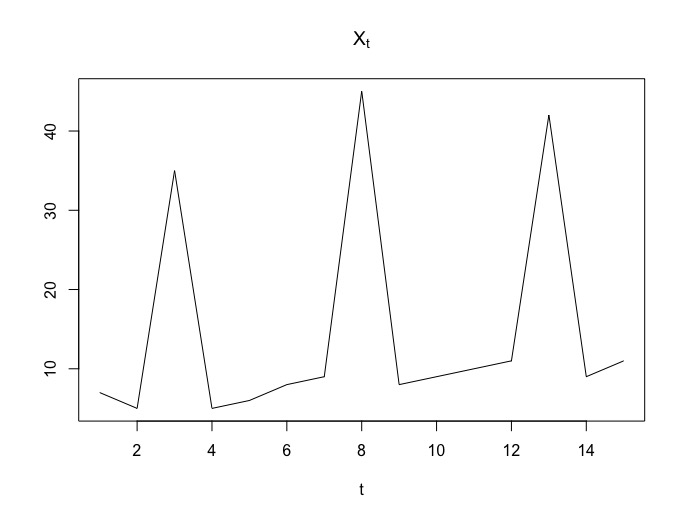
On choisit un modèle additif car les différences (maximum-minimum) semblent similaires sur chaque période (semaine). Les termes tendanciels pour  $\$\backslash (t\backslash in\backslash left\backslash \{\; 3,\backslash dots,13\backslash right\backslash \}\backslash )\$$ figurent dans le tableau ci-après.

On utilise la moyenne mobile $\$\backslash (M\_\{5\}\backslash )\$$ afin d’estimer la tendance (supposée linéaire) de la série temporelle. Pour rappel cette moyenne mobile conserve les tendances linéaires et absorbe les saisonnalités de période 5.

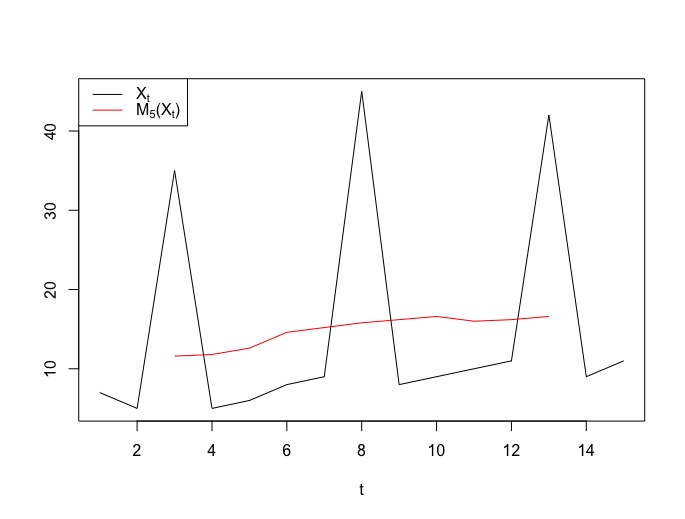
On calcule les coefficients saisonniers comme suit :

$\$\backslash [c\_\{mercredi\}\backslash frac\{23,4+29,2+25,4\}\{3\}=26\backslash \; \backslash \backslash \; c\_\{jeudi\}\backslash frac\{-6,8-8,2\}\{2\}=-7,5\backslash \; \backslash \backslash \; c\_\{vendredi\}\backslash frac\{-6,6-7,6\}\{2\}=-7,1\backslash \; \backslash \backslash \; c\_\{lundi\}\backslash frac\{-6,6-6\}\{2\}=-6,3\backslash \; \backslash \backslash \; c\_\{mardi\}\backslash frac\{-6,2-5,2\}\{2\}=-5,7\backslash \; \backslash ]\$$

On constate que :

$\$\backslash [\backslash overline\{c\}=-0,12\backslash \backslash ]\$$

Les coefficients saisonniers centrés sont :

$\$\backslash [c\_\{mercredi\}^\backslash prime\; =26-(-0,12)=26,12\backslash \; ,\backslash \backslash \; c\_\{jeudi\}^\backslash prime\; =-7,5-(-0,12)=-7,38\backslash \; ,\backslash \backslash \; c\_\{vendredi\}^\backslash prime\; =-7,1-(-0,12)=-6,98\backslash \; ,\backslash \backslash \; c\_\{lundi\}^\backslash prime\; =-6,3-(-0,12)=-6,18\backslash \; ,\backslash \backslash \; c\_\{mardi\}^\backslash prime\; =-5,7-(-0,12)=-5,58\backslash \; \backslash ]\$$

La série corrigée des variations saisonnières, est ainsi représentée :

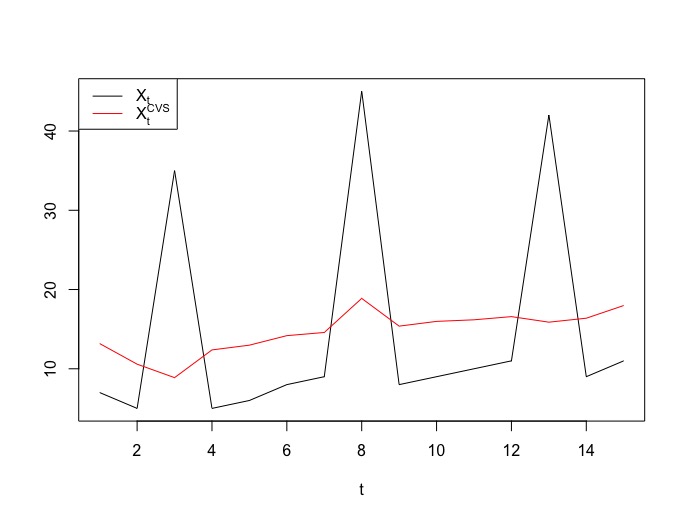
TP : Désaisonnaliser une série temporelle à l’aide de la fonction decompose

On utilise la fonction `decompose` :

decomp.x=decompose(x,type="multiplicative")
plot(decomp.x)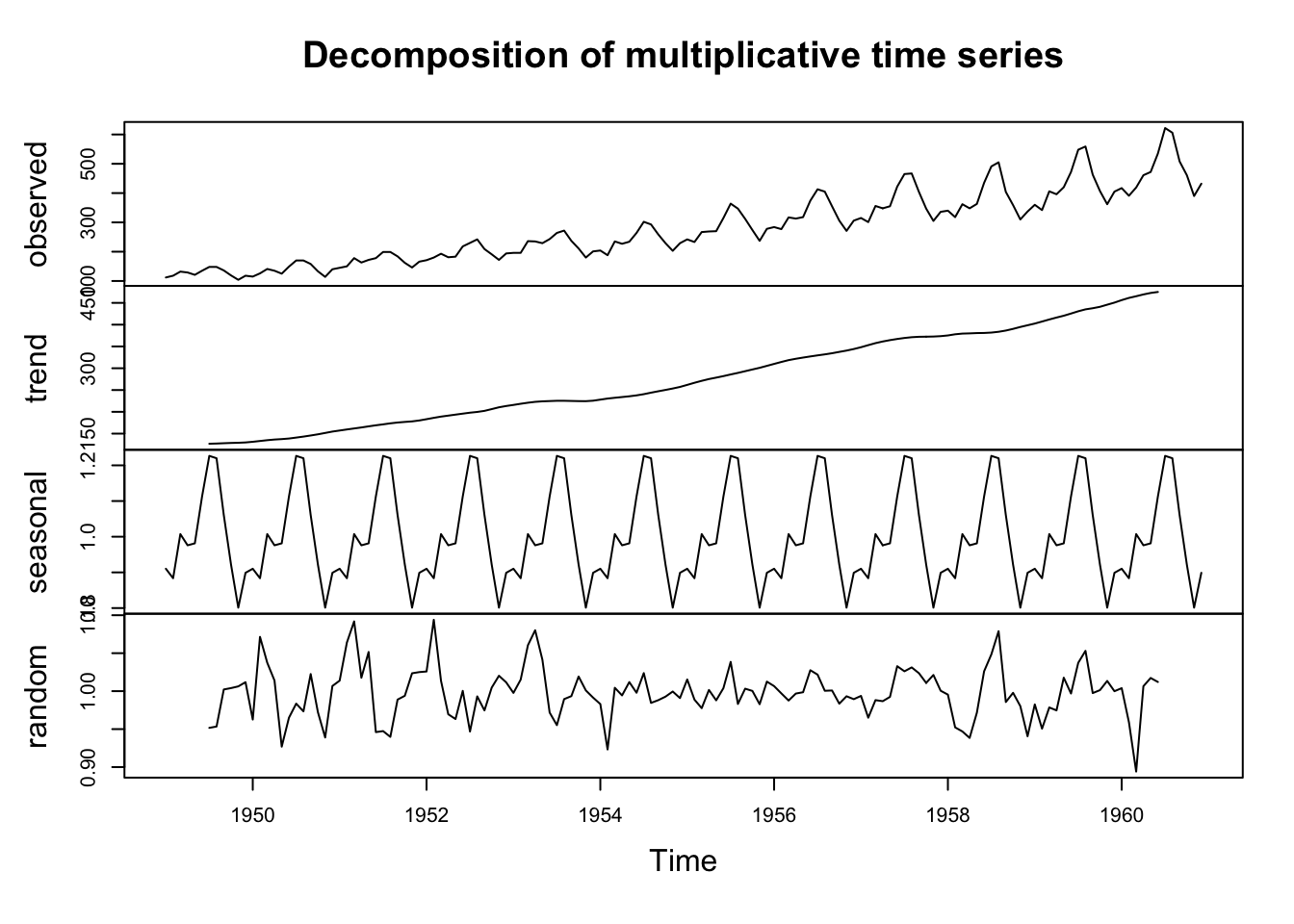

Pour aller plus loin : l’algorithme X11

Il existe aujourd’hui de nombreux algorithmes élaborés pour corriger les séries tempo-
relles des variations saisonnières. Nous n’entrerons pas dans le détail de ces méthodes mais
présentons ici un de ces représentants les plus simples, l’algorithme X11 développé par le
Census Bureau. Il s’agit d’un algorithme qui procède à une estimation de la série corrigée
des variations saisonnières en 2 phases de 4 étapes chacune.
Considérons une série temporelle répondant au modèle additif classique, avec une tendance
linéaire et une saisonnalité de période 12 (il existe plusieurs versions de cet algorithme :
pour les modèles additifs et multiplicatifs, pour des séries trimestrielles ou mensuelles, avec
une saisonnalité annuelle) :

$\$\backslash [X\_\{t\}=T\_\{t\}+S\_\{t\}+\backslash varepsilon\_\{t\}\backslash \; .\backslash ]\$$

1. Primo-estimation de la tendance

$\$\backslash [\backslash widehat\{T\}\_\{t\}^\{(1)\}=M\_\{2\backslash times12\}X\_\{t\}\backslash ]\$$

(sur le même principe que la méthode simplifiée vue auparavant).

2. Primo-estimation de la somme composante saisonnière-perturbation
En notant $\$\backslash (\backslash Sigma\_\{t\}=S\_\{t\}+\backslash varepsilon\_\{t\}\backslash )\$$  :

$\$\backslash [\backslash widehat\{\backslash Sigma\}\_\{t\}^\{(1)\}=X\_\{t\}-\backslash widehat\{T\}\_\{t\}^\{(1)\}\backslash ]\$$

(on retranche simplement la primo-estimation de la tendance à la série de départ).

3. Primo-estimation de la composante saisonnière

$\$\backslash [\backslash widehat\{S\}\_\{t\}^\{(1)\}=\backslash left(I-M\_\{2\backslash times\; 12\}\backslash right)\backslash left(M\_\{3\}\backslash right)^2\backslash widehat\{\backslash Sigma\}\_\{t\}^\{(1)\}\backslash ]\$$

(les coefficients sont ainsi normalisés afin que leur somme soit nulle sur une période
de 12 instants consécutifs).

4. Primo-estimation de la série corrigée des variations saisonnières

$\$\backslash [X\_\{t\}^\{CVS(1)\}=X\_\{t\}-\backslash widehat\{S\}\_\{t\}^\{(1)\}\backslash ]\$$

(on retranche la saisonnalité estimée à la série de départ).
5. Estimation définitive de la tendance

$\$\backslash [\backslash widehat\{T\}\_\{t\}^\{(2)\}=M\_\{13\}^H\; X\_\{t\}^\{CVS(1)\}\backslash ]\$$

(on utilise une moyenne mobile, nommée de Henderson d’ordre FORMULE_MATH afin d’extraire une seconde tendance à partir de la première série corrigée des variations saisonnières).
6. Estimation définitive de la somme composante saisonnière-perturbation (2)

$\$\backslash [\backslash widehat\{\backslash Sigma\}\_\{t\}^\{(2)\}=X\_\{t\}-\backslash widehat\{T\}\_\{t\}^\{(2)\}\backslash ]\$$

(on retrouve ici la même procédure que précédemment).

7. Estimation définitive de la composante saisonnière

$\$\backslash [\backslash widehat\{S\}\_\{t\}^\{(2)\}=\backslash left(I-M\_\{2\backslash times\; 12\}\backslash right)\; M\_\{3\}M\_\{5\}\backslash widehat\{\backslash Sigma\}\_\{t\}^\{(2)\}\backslash ]\$$

(on retrouve ici un lissage et une normalisation de la composante saisonnière).
8. Estimation définitive de la série corrigée des variations saisonnières (2)

$\$\backslash [X\_\{t\}^\{CVS(2)\}=X\_\{t\}-\backslash widehat\{S\}\_\{t\}^\{(2)\}\backslash ]\$$

(on retranche la seconde saisonnalité estimée à la série de départ, cette étape clôt
l’algorithme).