Calculez le montant des intérêts : la capitalisation
Nous venons de travailler sur un calcul simple d’intérêt qui suffit souvent dans de nombreuses opérations. Il se peut néanmoins que vous ayez à calculer ou expliquer le principe des taux composés ou capitalisés.
Ce principe est relativement intuitif, il vous suffit de :
Calculer un montant d’intérêt sans le rembourser au créancier,
Le réintégrer au capital en cours pour la période suivante, et ce autant de fois que nécessaire,
Verser la totalité des intérêts en fin d’opération.
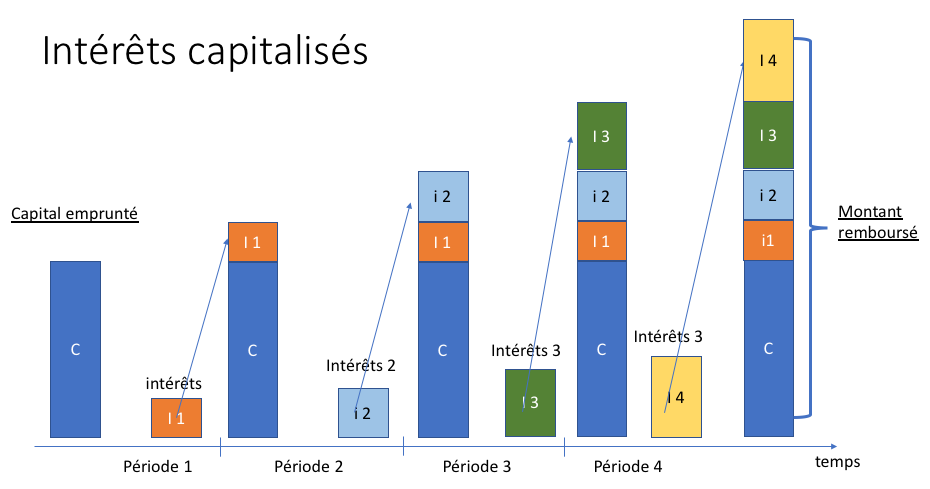
Prenons un exemple. Vous empruntez 1 000 € sur 5 ans au total à un taux de 5% en base obligataire. Les montants d’intérêts seront composés/capitalisés tout au long de la période.
Au bout d’un an, par la formule des intérêts simples, le créancier devrait toucher :
Le nouveau montant de la créance sur la seconde année est donc du capital majoré des intérêts qui viennent d’être calculés :
Souvenez vous de vos cours de 4ième, le capital est le facteur commun… ;)
Puisque le capital vaut 1 000 dans notre exemple, le total est de 1 050 €. Au bout de la seconde année, le montant d’intérêt calculé est de :
Comme l’année précédente, le montant sera réintégré à la créance. Le nouveau montant de la créance est donc de Capital x (1 + 0,05)(1 + 0,05) soit 1 102,50 €.
Si on va jusqu’au bout de la 5ième année, l’intérêt final du est de :
On en tire la formule d’intérêts composés pour notre exemple :
ou de manière plus générale sur n années :
Cette formule de capitalisation des intérêts sera par exemple appliquée lorsque vous mettrez en place un prêt pour acheter un appartement neuf avec une franchise totale. Une franchise totale, c’est une période pendant laquelle le client ne paiera que ses assurances. Les intérêts dus chaque mois ne seront pas payés mais ajoutés au capital initialement emprunté. Vous vous en doutez, cette opération pose une question de garantie, mais nous en reparlerons.
Utilisez la formule d'intérêts composés
Cette formule va vous être utile pour estimer la valeur future d’un investissement. Vous allez utiliser la même logique.
Par exemple, si vous investissez 100 000 € aujourd’hui à un taux capitalisé annuellement de 3% sur une durée de 6 ans ½, quelle sera la valeur finale de notre investissement ?
soit une valeur future de 121 183,07 €.
Le taux d’intérêt utilisé s’appelle le taux de capitalisation.
Ce type de calcul pourra vous être utile lorsque vous aurez par exemple à calculer quel sera le montant en cours sur une assurance-vie en fonds EURO (donc à priori sans risque en capital) dans n années. Il suffira d’estimer un rendement moyen en fonction des taux actuels et de capitaliser sur n années. Ce calcul pourra également vous être utile pour estimer les capacités de remboursement d’un crédit dont la garantie est constituée non pas par une sûreté réelle mais par de l’épargne, en l'occurrence un contrat d’assurance-vie en Euros.
Maintenant, si on rend les choses un peu plus complexes et que l’on intègre un versement régulier sur notre assurance-vie. Quel capital peut-on espérer en fin de période de capitalisation ? Voici la formule qui va pouvoir vous aider :
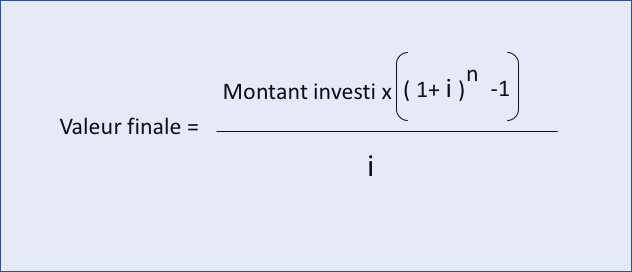
Il vous faut également préciser quel sera la fréquence des versements d’épargne. Seront-ils annuels, semestriels, trimestriels ou mensuels ? La réponse à cette question déterminera le taux i à renseigner car i est un taux annuel et s’il faut réaliser des versements mensuels il faut le diviser par 12. Si ce sont des versement trimestriels, il faut le diviser par 4 etc.
Essayez avec quelques cas concrets
Vous souhaitez savoir quel sera le montant final d’un investissement de 300 € mensuels fait sur une durée de 15 ans à un taux fixe de 2%. Les intérêts seront calculés et capitalisés mensuellement.
Valeur finale = 300 € x ((1+2%/12)^(15x12) -1)/(2%/12)= 62 913,92
2. Maintenant, mettez-vous dans la situation suivante : un client souhaite ouvrir une assurance-vie dont le montant initial sera de 10 000 € et sur laquelle il souhaite investir 300 € mensuellement. Il vous demande d’estimer quel sera le montant dont il devrait pouvoir bénéficier (hors fiscalité) dans 15 ans. Votre estimation prudente des taux d’intérêts distribués par des fonds Euro dans les 15 ans qui viennent est de 1%. Quelle sera votre réponse ?
Il faut ici raisonner en deux parties :
La capitalisation du capital initial donne € 11 617,52
La capitalisation des 300 € versés chaque mois pendant 15 ans est de € 58 234,20
Au total, il peut donc espérer disposer de presque 70 000 € dans 15 ans.
Maintenant que vous avez estimé la valeur future d’un flux actuel, vous pouvez également souhaiter estimer la valeur actuelle d’un flux futur : c'est ce que nous allons voir avec l'actualisation.
L'actualisation
Si vous pouvez vous projeter vers le futur, vous pouvez également faire machine arrière et partir du futur pour estimer le présent. C’est possible et c’est ce que l’on appelle l’actualisation.
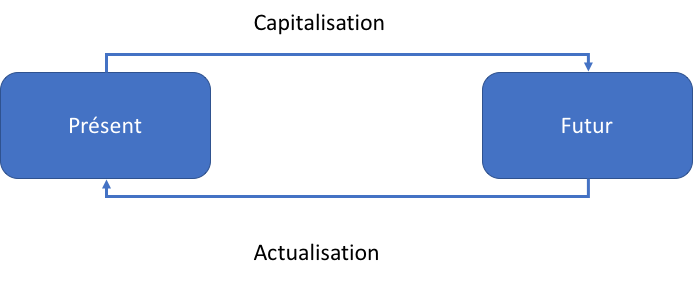
Il suffit pour cela de faire le parcours dans le sens inverse et donc de mettre un signe négatif à la puissance dans la formule de capitalisation.
Vous aurez donc :
L'exemple de l'assurance-vie
Pour reprendre l’exemple de l’assurance-vie, demandez-vous quel serait le montant à investir aujourd’hui sur un fonds EURO avec un rendement annuel moyen estimé à 1,5% afin d’atteindre 100 000 € au bout de 15 ans.
Le résultat serait donc 79 985,15 €
Cela veut également dire que si vous investissez 79 985,15 € sur une obligation ne détachant pas de revenus mais capitalisant un intérêt de 1,5% pendant 15 ans, vous devriez être remboursés de 100 000 € en fin de période.
Vous l’avez compris, cela ne veut pas dire que la rémunération de l’obligation est de zéro % mais que le taux d’intérêt n’est pas distribué régulièrement mais bel et bien capitalisé et versé dans sa totalité à l’échéance.
En résumé
Le principe des taux composés ou capitalisés est le suivant :
calculer un montant d'intérêt sans le rembourser au créancier ;
le réintégrer au capital en cours pour la période suivant, et ce, autant de fois que nécessaire ;
verser la totalité des intérêts en fin d'opération.
Dans la prochaine partie, nous verrons comment calculer les taux d'intérêt lors d'un crédit immobilier. Mais avant d'y être, testez vos connaissances avec ce quizz.
