Mensualités linéaires et mensualités constantes
Lors d’un remboursement de prêt, deux solutions sont possibles pour rembourser à l’établissement prêteur le capital emprunté.
Les mensualités linéaires
La première invite l’emprunteur à rembourser son capital de manière linéaire. Ce remboursement peut être mensuel, trimestriel, semestriel ou annuel. Bien sûr, on ne parle pas ici de prêts « in fine » dans lesquels le capital emprunté est remboursé en totalité à l’échéance du prêt. C
Ainsi, si vous empruntez 10 000 € sur 3 ans (36 mois), et que vous choisissez un remboursement linéaire mensuel du capital, vous devrez rembourser chaque mois, en plus des intérêts 10 000 € / 36 soit 277,78 €.
Les mensualités constantes
Cette seconde solution est largement utilisée dans le monde bancaire car elle permet aux emprunteurs de maîtriser leurs mensualités et aux prêteurs d’être en mesure d’annoncer un montant qui ne changera jamais au cours du prêt. Bien entendu tout ceci ne marche que si nous sommes dans un environnement de taux fixes. Ce souci de la sécurité est omniprésent dans la tête des ménages, surtout en termes d’endettement.
Calculez les mensualités constantes
Comment faire pour obtenir des mensualités, trimestrialités, semestrialités ou annuités constantes ?
Il faut bien sûr faire en sorte de rembourser au départ un montant faible de capital qui va augmenter au cours du temps. Le capital diminuant petit à petit, le montant d’intérêts calculé sera de plus en plus faible et on pourra donc rembourser de plus en plus de capital.
Comment “jongler” avec toutes ces informations ?
Comme souvent, les mathématiques nous aident ! La formule de calcul du montant correspondant au remboursement constant d'un crédit est :
Dans cette formule :
C = le capital emprunté
t = le taux annuel nominal du prêt
n = le nombre de paiements sur la durée totale du prêt
f = nombre de paiements sur une année ( 12 si on calcule des mensualités, 4 pour des trimestrialités, 2 pour des semestrialités et 1 pour les annuités)
Ainsi si on cherche le remboursement d’un prêt à 5 ans une fois par an, on utilisera et
Fréquemment, lorsque l’on calcule des mensualités constantes,
f= 12
et n= 12 x nombre d’années du prêt
Ainsi, en appliquant cette formule, quelle sera la mensualité constante d’un prêt de 200 000 € à 2% sur 10 ans ?
On applique :
Soit un résultat de 1 840,27 € (voir impression tableur ci-dessous).
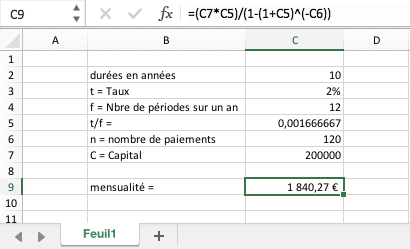
Cette formule permet de refaire les calculs ci-dessus plus rapidement.
Il suffit juste de remplir les arguments correctement comme suit :
Ainsi, si on rentre =VPM(2%/12;120;200000) et on obtient 1 840,27 €.
En résumé
Les mensualités constantes : prêt à taux et à mensualités fixes. Le montant des mensualités reste le même pendant toute la durée du prêt.
Les mensualités linéaires : il ne s'agit plus de payer le même montant à intervalle régulier pendant toute la durée de l'emprunt mais de rembourser la même part du capital emprunté à chaque échéance.
La différence entre les mensualités constantes et linéaires sont posées. Nous allons voir maintenant comment dissocier les intérêts du capital dans les mensualités constantes.
